题目内容
请你利用直角坐标平面上任意两点(x1,y1)、(x2,y2)间的距离公式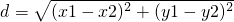 解答下列问题:
解答下列问题:
已知:反比例函数 与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(-2,-2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数
与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(-2,-2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数 图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1-PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1-PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
解:解由 和y=x组成的方程组可得A、B两点的坐标分别为,(
和y=x组成的方程组可得A、B两点的坐标分别为,( ,
, )、(
)、(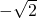 ,
,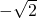 ),线段AB的长度=4
),线段AB的长度=4
∵点P(x0,y0)是反比例函数 图象上一点,
图象上一点,
∴y0=
∴PF1=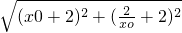 =
=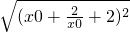 =|
=| |,
|,
PF2= =
=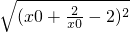 =|
=|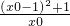 |,
|,
∴d=|PF1-PF2|=|| |-|
|-|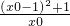 ||,
||,
当x0>0时,d=4;当x0<0时,d=4.
因此,无论点P的位置如何,线段AB的长度与d一定相等.
由此可知:到两个定点的距离之差(取正值)是定值的点的集合(轨迹)是双曲线.
分析:解由 和y=x组成的方程组可得A、B两点的坐标分别为(
和y=x组成的方程组可得A、B两点的坐标分别为( ,
, )、(
)、(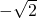 ,
,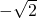 ),利用两点间的距离公式可求出线段AB的长度,由P为反比例函数y=
),利用两点间的距离公式可求出线段AB的长度,由P为反比例函数y= 上一点可得出x0与y0的关系式,利用两点间的距离公式可得出PF1、PF2的长,代入d=|PF1-PF2|即可得到x0的表达式,再根据x0的取值范围即可求出d的长,进而得出结论.
上一点可得出x0与y0的关系式,利用两点间的距离公式可得出PF1、PF2的长,代入d=|PF1-PF2|即可得到x0的表达式,再根据x0的取值范围即可求出d的长,进而得出结论.
点评:本题考查的是反比例函数与一次函数的交点问题,熟练利用两点间的距离公式是解答此题的关键.
 和y=x组成的方程组可得A、B两点的坐标分别为,(
和y=x组成的方程组可得A、B两点的坐标分别为,( ,
, )、(
)、(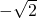 ,
,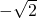 ),线段AB的长度=4
),线段AB的长度=4∵点P(x0,y0)是反比例函数
 图象上一点,
图象上一点,∴y0=

∴PF1=
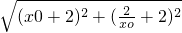 =
=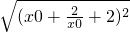 =|
=| |,
|,PF2=
 =
=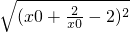 =|
=|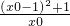 |,
|,∴d=|PF1-PF2|=||
 |-|
|-|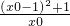 ||,
||,当x0>0时,d=4;当x0<0时,d=4.
因此,无论点P的位置如何,线段AB的长度与d一定相等.
由此可知:到两个定点的距离之差(取正值)是定值的点的集合(轨迹)是双曲线.
分析:解由
 和y=x组成的方程组可得A、B两点的坐标分别为(
和y=x组成的方程组可得A、B两点的坐标分别为( ,
, )、(
)、(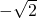 ,
,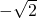 ),利用两点间的距离公式可求出线段AB的长度,由P为反比例函数y=
),利用两点间的距离公式可求出线段AB的长度,由P为反比例函数y= 上一点可得出x0与y0的关系式,利用两点间的距离公式可得出PF1、PF2的长,代入d=|PF1-PF2|即可得到x0的表达式,再根据x0的取值范围即可求出d的长,进而得出结论.
上一点可得出x0与y0的关系式,利用两点间的距离公式可得出PF1、PF2的长,代入d=|PF1-PF2|即可得到x0的表达式,再根据x0的取值范围即可求出d的长,进而得出结论.点评:本题考查的是反比例函数与一次函数的交点问题,熟练利用两点间的距离公式是解答此题的关键.

练习册系列答案
相关题目
 解答下列问题:
解答下列问题: 图象上的任意一点,记点P与F1、F2两点的距离之差
图象上的任意一点,记点P与F1、F2两点的距离之差