ΧβΡΩΡΎ»ί
«κΡψάϊ”Ο÷±Ϋ«Ήχ±ξΤΫΟφ…œ»Έ“βΝΫΒψΘ®x1Θ§y1Θ©ΓΔΘ®x2Θ§y2Θ©ΦδΒΡΨύάκΙΪ Ϋd=| (x1-x2)2+(y1-y2)2 |
“―÷ΣΘΚΖ¥±»άΐΚ· ΐy=
| 2 |
| x |
| 2 |
| x |
Ζ÷ΈωΘΚΫβ”…y=
ΚΆy=xΉι≥…ΒΡΖΫ≥ΧΉιΩ…ΒΟAΓΔBΝΫΒψΒΡΉχ±ξΖ÷±πΈΣΘ®
Θ§
Θ©ΓΔΘ®-
Θ§-
Θ©Θ§άϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ ΫΩ…«σ≥ωœΏΕΈABΒΡ≥ΛΕ»Θ§”…PΈΣΖ¥±»άΐΚ· ΐy=
…œ“ΜΒψΩ…ΒΟ≥ωx0”κy0ΒΡΙΊœΒ ΫΘ§άϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ ΫΩ…ΒΟ≥ωPF1ΓΔPF2ΒΡ≥ΛΘ§¥ζ»κd=|PF1-PF2|Φ¥Ω…ΒΟΒΫx0ΒΡ±μ¥ο ΫΘ§‘ΌΗυΨίx0ΒΡ»Γ÷ΒΖΕΈßΦ¥Ω…«σ≥ωdΒΡ≥ΛΘ§ΫχΕχΒΟ≥ωΫα¬έΘ°
| 2 |
| x |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| x |
Ϋβ¥πΘΚΫβΘΚΫβ”…y=
ΚΆy=xΉι≥…ΒΡΖΫ≥ΧΉιΩ…ΒΟAΓΔBΝΫΒψΒΡΉχ±ξΖ÷±πΈΣΘ§Θ®
Θ§
Θ©ΓΔΘ®-
Θ§-
Θ©Θ§œΏΕΈABΒΡ≥ΛΕ»=4Θ®2Ζ÷Θ©
ΓΏΒψPΘ®x0Θ§y0Θ© «Ζ¥±»άΐΚ· ΐy=
ΆΦœσ…œ“ΜΒψΘ§
Γύy0=
ΓύPF1=
=
=|
|Θ§
PF2=
=
=|
|Θ§Θ®3Ζ÷Θ©
Γύd=|PF1-PF2|=||
|-|
||Θ§
Β±x0ΘΨ0 ±Θ§d=4ΘΜΒ±x0ΘΦ0 ±Θ§d=4Θ°Θ®3Ζ÷Θ©
“ρ¥ΥΘ§Έό¬έΒψPΒΡΈΜ÷Ο»γΚΈΘ§œΏΕΈABΒΡ≥ΛΕ»”κd“ΜΕ®œύΒ»Θ°Θ®2Ζ÷Θ©
”…¥ΥΩ…÷ΣΘΚΒΫΝΫΗωΕ®ΒψΒΡΨύάκ÷°≤νΘ®»Γ’ΐ÷ΒΘ© «Ε®÷ΒΒΡΒψΒΡΦ·ΚœΘ®ΙλΦΘΘ© «ΥΪ«ζœΏΘ°Θ®2Ζ÷Θ©
| 2 |
| x |
| 2 |
| 2 |
| 2 |
| 2 |
ΓΏΒψPΘ®x0Θ§y0Θ© «Ζ¥±»άΐΚ· ΐy=
| 2 |
| x |
Γύy0=
| 2 |
| x0 |
ΓύPF1=
(x0+2)2+(
|
(x0+
|
| (x0+1)2+1 |
| x0 |
PF2=
(x0-2)2+(
|
(x0+
|
| (x0-1)2+1 |
| x0 |
Γύd=|PF1-PF2|=||
| (x0+1)2+1 |
| x0 |
| (x0-1)2+1 |
| x0 |
Β±x0ΘΨ0 ±Θ§d=4ΘΜΒ±x0ΘΦ0 ±Θ§d=4Θ°Θ®3Ζ÷Θ©
“ρ¥ΥΘ§Έό¬έΒψPΒΡΈΜ÷Ο»γΚΈΘ§œΏΕΈABΒΡ≥ΛΕ»”κd“ΜΕ®œύΒ»Θ°Θ®2Ζ÷Θ©
”…¥ΥΩ…÷ΣΘΚΒΫΝΫΗωΕ®ΒψΒΡΨύάκ÷°≤νΘ®»Γ’ΐ÷ΒΘ© «Ε®÷ΒΒΡΒψΒΡΦ·ΚœΘ®ΙλΦΘΘ© «ΥΪ«ζœΏΘ°Θ®2Ζ÷Θ©
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΒΡ «Ζ¥±»άΐΚ· ΐ”κ“Μ¥ΈΚ· ΐΒΡΫΜΒψΈ ΧβΘ§ λΝΖάϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ Ϋ «Ϋβ¥π¥ΥΧβΒΡΙΊΦϋΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
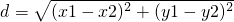 Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Ϋβ¥πœ¬Ν–Έ ΧβΘΚ ”κ’ΐ±»άΐΚ· ΐy=xΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψΘ®A‘ΎΒΎ“ΜœσœόΘ©Θ§ΒψF1Θ®-2Θ§-2Θ©ΓΔF2Θ®2Θ§2Θ©‘Ύ÷±œΏy=x…œΘ°…ηΒψPΘ®x0Θ§y0Θ© «Ζ¥±»άΐΚ· ΐ
”κ’ΐ±»άΐΚ· ΐy=xΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψΘ®A‘ΎΒΎ“ΜœσœόΘ©Θ§ΒψF1Θ®-2Θ§-2Θ©ΓΔF2Θ®2Θ§2Θ©‘Ύ÷±œΏy=x…œΘ°…ηΒψPΘ®x0Θ§y0Θ© «Ζ¥±»άΐΚ· ΐ Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Ϋβ¥πœ¬Ν–Έ ΧβΘΚ ΆΦœσ…œΒΡ»Έ“β“ΜΒψΘ§Φ«ΒψP”κF1ΓΔF2ΝΫΒψΒΡΨύάκ÷°≤ν
ΆΦœσ…œΒΡ»Έ“β“ΜΒψΘ§Φ«ΒψP”κF1ΓΔF2ΝΫΒψΒΡΨύάκ÷°≤ν