题目内容
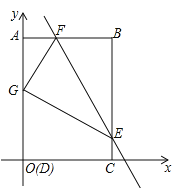
【题目】如图,四边形ABCD为矩形,C点在![]() 轴上,A点在
轴上,A点在![]() 轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).
轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).
(1)求G点坐标
(2)求直线EF解析式
(3)点N在坐标轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,直接写出M点坐标;若不存在,请说明理由
【答案】(1)G(0,4-![]() );(2)
);(2)![]() ;(3)
;(3) .
.
【解析】
1(1)由F(1,4),B(3,4),得出AF=1,BF=2,根据折叠的性质得到GF=BF=2,在Rt△AGF中,利用勾股定理求出![]() ,那么OG=OA-AG=4-
,那么OG=OA-AG=4-![]() ,于是G(0,4-
,于是G(0,4-![]() );
);
(2)先在Rt△AGF中,由![]() ,得出∠AFG=60°,再由折叠的性质得出∠GFE=∠BFE=60°,解Rt△BFE,求出BE=BF
,得出∠AFG=60°,再由折叠的性质得出∠GFE=∠BFE=60°,解Rt△BFE,求出BE=BF![]() tan60°=2
tan60°=2![]() ,那么CE=4-2
,那么CE=4-2![]() ,E(3,4-2
,E(3,4-2![]() ).设直线EF的表达式为y=kx+b,将E(3,4-2
).设直线EF的表达式为y=kx+b,将E(3,4-2![]() ),F(1,4)代入,利用待定系数法即可求出直线EF的解析.(3)因为M、N均为动点,只有F、G已经确定,所以可从此入手,结合图形,按照FG为一边,N点在x轴上;FG为一边,N点在y轴上;FG为对角线的思路,顺序探究可能的平行四边形的形状.确定平行四边形的位置与形状之后,利用平行四边形及平移的性质求得M点的坐标.
),F(1,4)代入,利用待定系数法即可求出直线EF的解析.(3)因为M、N均为动点,只有F、G已经确定,所以可从此入手,结合图形,按照FG为一边,N点在x轴上;FG为一边,N点在y轴上;FG为对角线的思路,顺序探究可能的平行四边形的形状.确定平行四边形的位置与形状之后,利用平行四边形及平移的性质求得M点的坐标.
解:(1)∵F(1,4),B(3,4),
∴AF=1,BF=2,
由折叠的性质得:GF=BF=2,
在Rt△AGF中,由勾股定理得,
![]()
∵B(3,4),
∴OA=4,
∴OG=4-![]() ,
,
∴G(0,4-![]() );
);
(2)在Rt△AGF中,
∵![]() ,
,
∴∠AFG=60°,由折叠的性质得知:∠GFE=∠BFE=60°,
在Rt△BFE中,
∵BE=BF![]() tan60°=2
tan60°=2![]() ,
,
.CE=4-2![]() ,
,
.E(3,4-2![]() ).
).
设直线EF的表达式为y=kx+b,
∵E(3,4-2![]() ),F(1,4),
),F(1,4),
∴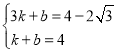 解得
解得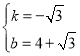
∴![]() ;
;

(3)若以M、N、F、G为顶点的四边形是平行四边形,则分如下四种情况:
①FG为平行四边形的一边,N点在x轴上,GFMN为平行四边形,如图1所示.
过点G作EF的平行线,交x轴于点N1,再过点N:作GF的平行线,交EF于点M,得平行四边形GFM1N1.
∵GN1∥EF,直线EF的解析式为![]()
∴直线GN1的解析式为![]() ,
,
当y=0时,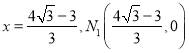 .
.
∵GFM1N1是平行四边形,且G(0,4-![]() ),F(1,4),N1(
),F(1,4),N1(![]() ,0),
,0),
∴M,(![]() ,
,![]() );
);
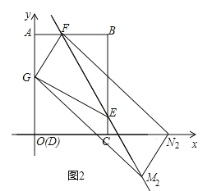
②FG为平行四边形的一边,N点在x轴上,GFNM为平行四边形,如图2所示.
∵GFN2M2为平行四边形,
∴GN与FM2互相平分.
∴G(0,4-![]() ),N2点纵坐标为0
),N2点纵坐标为0
∴GN:中点的纵坐标为![]() ,
,
设GN中点的坐标为(x,![]() ).
).
∵GN2中点与FM2中点重合,
∴![]()
∴x=![]()
∵.GN2的中点的坐标为(![]() ),
),
.∴N2点的坐标为(![]() ,0).
,0).
∵GFN2M2为平行四边形,且G(0,4-![]() ),F(1,4),N2(
),F(1,4),N2(![]() ,0),
,0),
∴M2(![]() );
);

③FG为平行四边形的一边,N点在y轴上,GFNM为平行四边形,如图3所示.
∵GFN3M3为平行四边形,.
∴GN3与FM3互相平分.
∵G(0,4-![]() ),N2点横坐标为0,
),N2点横坐标为0,
.∴GN3中点的横坐标为0,
∴F与M3的横坐标互为相反数,
∴M3的横坐标为-1,
当x=-1时,y=![]() ,
,
∴M3(-1,4+2![]() );
);
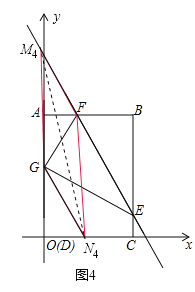
④FG为平行四边形的对角线,GMFN为平行四边形,如图4所示.
过点G作EF的平行线,交x轴于点N4,连结N4与GF的中点并延长,交EF于点M。,得平行四边形GM4FN4
∵G(0,4-![]() ),F(1,4),
),F(1,4),
∴FG中点坐标为(![]() ),
),
∵M4N4的中点与FG的中点重合,且N4的纵坐标为0,
.∴M4的纵坐标为8-![]() .
.
5-45解方程![]() ,得
,得![]()
∴M4(![]() ).
).
综上所述,直线EF上存在点M,使以M,N,F,G为顶点的四边形是平行四边形,此时M点坐标为: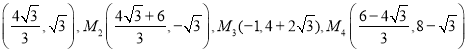 。
。

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克) | ﹣4 | ﹣2 | 0 | 1 | 3 | 6 |
个数 | 10 | 13 | 30 | 25 | 15 | 7 |
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
【题目】某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信,这五封信的重量分别是![]() .根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
业务种类 | 计费单位 | 资费标准/元 | 挂号费/(元/封) | 特制信封(元/个) |
挂号信 | 首重100g,每重20g | 0.8 | 3 | 0.5 |
续重101~2000g,每重100g | 2.00 | |||
特制信封 | 首重1000g内 | 5.00 | 3 | 1.0 |
(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?
(2)这五封信分别以怎样的方式寄出最合算?请说明理由.
(3)通过解答上述问题,你有何启示?(请你用一两句话说明)