题目内容
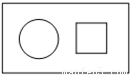
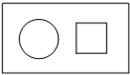 向如图所示的周长相等的圆和正方形区域内做投针实验,命中圆的概率与命中正方形的概率分别为P1、P2,则
向如图所示的周长相等的圆和正方形区域内做投针实验,命中圆的概率与命中正方形的概率分别为P1、P2,则
- A.P1>P2
- B.P1=P2
- C.P1<P2
- D.P1=2P2
C
分析:首先设圆的半径为r,表示出圆的周长和圆的面积,再设正方形的边长为x,根据圆和正方形的周长相等用含r的式子表示出x,再表示出正方形的面积,然后比较面积的大小即可得到P1、P2的大小.
解答:设圆的半径为r,则圆的周长为:2πr,
圆的面积为:πr2,
设正方形的边长为x,
∵圆和正方形的周长相等,
∴4x=2πr,
x=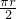 ,
,
∴正方形的面积为: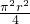 ,
,
∵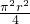 >πr2,
>πr2,
∴P1<P2.
故选:C.
点评:此题主要考查了概率,关键是表示出正方形和圆的面积,根据面积的大小即可比较出概率的大小.
分析:首先设圆的半径为r,表示出圆的周长和圆的面积,再设正方形的边长为x,根据圆和正方形的周长相等用含r的式子表示出x,再表示出正方形的面积,然后比较面积的大小即可得到P1、P2的大小.
解答:设圆的半径为r,则圆的周长为:2πr,
圆的面积为:πr2,
设正方形的边长为x,
∵圆和正方形的周长相等,
∴4x=2πr,
x=
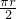 ,
,∴正方形的面积为:
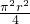 ,
,∵
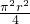 >πr2,
>πr2,∴P1<P2.
故选:C.
点评:此题主要考查了概率,关键是表示出正方形和圆的面积,根据面积的大小即可比较出概率的大小.

练习册系列答案
相关题目
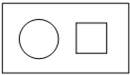 (2012•龙岩模拟)向如图所示的周长相等的圆和正方形区域内做投针实验,命中圆的概率与命中正方形的概率分别为P1、P2,则( )
(2012•龙岩模拟)向如图所示的周长相等的圆和正方形区域内做投针实验,命中圆的概率与命中正方形的概率分别为P1、P2,则( )