题目内容
【题目】如图，点A的坐标为（2，2），若点P在坐标轴上，且△APO为等腰三角形，则满足条件的点P个数是（ ）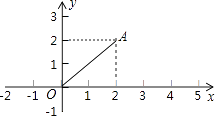
A.4个
B.6个
C.7个
D.8个
【答案】D
【解析】解：已知点A的坐标为（2，2），则△OAP的边OA=2 
，这条边可能是底边也可能是腰．
①当OA是底边时，点P是OA的垂直平分线与坐标轴的交点，这两个点的坐标是（2，0）和（0，2）；
②当OA是腰时，当O是顶角顶点时，以O为圆心，以OA为半径作圆，与坐标轴的交点坐标是（2 ，0），（﹣2 ，0），（0，2 ），（0，﹣2 ）；
③当A是顶角顶点时，以A为圆心，以AO为半径作圆，与坐标轴的交点坐标是（4，0），（0，4）．
故满足条件的点P共有8个．
故D符合题意.
故答案为：D．
分P在坐标轴和OA是底边、OA是腰、A是顶角顶点来讨论求解.
练习册系列答案
天天向上口算本系列答案
相关题目
