题目内容
如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于点E,过点D作DF⊥AE,垂足为F,DF交A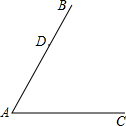 C于点G.
C于点G.(1)按要求在所给图中将图形补全,然后判断四边形ADEG的形状,并证明你的结论;
(2)标出有向线段
| AD |
| AF |
| AG |
| AD |
| a |
| AF |
| b |
| a |
| b |
| AG |
分析:(1)根据同位角相等,即可得DE∥AC;在作出∠BAC平分线,在作DF⊥AE,连接各点即可;根据已知易证AD=DE,AD=AG,又由DE∥AC,即可证得平行四边形ADEG为菱形;
(2)由菱形的性质与向量的意义,即可求得
=2
,继而求得向量
的值.
(2)由菱形的性质与向量的意义,即可求得
| AE |
| b |
| AG |
解答: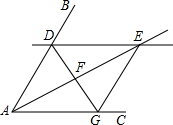 解:(1)四边形ADEG为菱形.
解:(1)四边形ADEG为菱形.
证明:∵DE∥AC,
∴∠DEA=∠EAC,
∵AE平分∠BAC,
∴∠DAE=∠EAC,
∴∠DAE=∠DEA,
∴DA=DE,
∵DF⊥AE,
∴AF=EF;
在△ADF和△AGF中,∠DAE=∠EAC,AF=AF,∠DFA=∠GFA=90°,
∴△ADF≌△AGF;
∴DF=GF,
∴四边形ADEG为平行四边形;
∵DF⊥AE,
∴平行四边形ADEG为菱形;

(2)∵
=
,
=
,四边形ADEG为菱形,
根据题意,得:
=2
,
∴
=
-
=2
-
,
∴
=
=-
+
.
 解:(1)四边形ADEG为菱形.
解:(1)四边形ADEG为菱形.证明:∵DE∥AC,
∴∠DEA=∠EAC,
∵AE平分∠BAC,
∴∠DAE=∠EAC,
∴∠DAE=∠DEA,
∴DA=DE,
∵DF⊥AE,
∴AF=EF;
在△ADF和△AGF中,∠DAE=∠EAC,AF=AF,∠DFA=∠GFA=90°,
∴△ADF≌△AGF;
∴DF=GF,
∴四边形ADEG为平行四边形;
∵DF⊥AE,
∴平行四边形ADEG为菱形;

(2)∵
| AD |
| a |
| AF |
| b |
根据题意,得:
| AE |
| b |
∴
| DE |
| AE |
| AD |
| b |
| a |
∴
| AG |
| DE |
| a |
| 2b |
点评:此题考查了学生的基本作图,以及菱形的判定定理和向量的知识.此题综合性很强,解题时要注意分析与识图.

练习册系列答案
相关题目
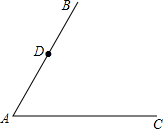 如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.
如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F. C于点G.
C于点G.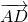 、
、 、
、 ,记向量
,记向量 、
、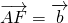 ,试用
,试用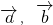 表示向量
表示向量 如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.
如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F. 、
、 、
、 ,记向量
,记向量 、
、 ,试用
,试用 表示向量
表示向量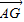 .
.