题目内容
 如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.
如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.
(1)按要求在右图上将图形补全;
(2)已知∠BAC=60°,AD=2,求线段EF的长.
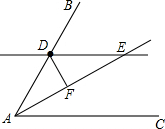 解:(1)如图
解:(1)如图(2)∵AE平分∠BAC,∠BAC=60°,
∴∠BAE=∠CAE=30°,
又∵DF⊥AE,AD=2,∴DF=1,
由勾股定理得

∵DE∥AC,∴∠DEA=∠CAE,
又∵∠BAE=∠CAE,∴∠BAE=∠DEA,
∴AD=DE
又∵DF⊥AE,
∴EF=AF=
 .
.分析:(1)按照题目给出的条件,先过点D作DE∥AC,然后作∠BAC平分线,交于E,再过点D作DF⊥AE,垂足为F.
(2)根据AE平分∠BAC,∠BAC=60°,DF⊥AE,AD=2,利用勾股定理求出AF的长,然后根据DE∥AC,DF⊥AE,求证EF=AF即可.
点评:此题主要考查学生对勾股定理和含30度角的直角三角形的理解和掌握,此题综合性较强,涉及到的知识点较多,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
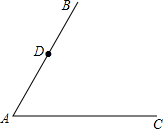 如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.
如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F. C于点G.
C于点G. C于点G.
C于点G.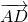 、
、 、
、 ,记向量
,记向量 、
、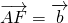 ,试用
,试用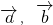 表示向量
表示向量 、
、 、
、 ,记向量
,记向量 、
、 ,试用
,试用 表示向量
表示向量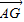 .
.