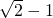题目内容
一个半径为r的圆内切于一个等腰直角三角形,另一个半径为R的圆外接于这个三角形,则
等于( )
| R |
| r |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
分析:根据题意得,等腰直角三角形的腰长为R+r,底边长为2R,再由勾股定理求得R与r的关系,将
看作整体,解关于
的一元二次方程即可得出答案.
| R |
| r |
| R |
| r |
解答:解:∵等腰直角三角形内切圆的半径为r,外接圆的半径为R,
∴等腰直角三角形的三边分别为R+r,R+r,2R,
∴由勾股定理得2(R+r)2=(2R)2,
整理得(
)2-2
-1=0,
则
=1±
(舍去负号).
故选A.
∴等腰直角三角形的三边分别为R+r,R+r,2R,
∴由勾股定理得2(R+r)2=(2R)2,
整理得(
| R |
| r |
| R |
| r |
则
| R |
| r |
| 2 |
故选A.
点评:本题是一道综合题,考查了等腰三角形的性质、三角形的内切圆和三角形的外接圆,难度较大.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
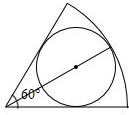 (2013•恩施州)如图所示,一半径为1的圆内切于一个圆心角为60°的扇形,则扇形的周长为
(2013•恩施州)如图所示,一半径为1的圆内切于一个圆心角为60°的扇形,则扇形的周长为
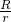 等于
等于 +1
+1