题目内容
解方程、计算与化简求值:(1)解方程
| 1 |
| x-1 |
| 2x |
| x+1 |
(2)计算 (-
| 1 |
| 2 |
| 7 |
(3)先化简代数式(
| x+2 |
| x2-2x |
| 1 |
| x-2 |
| 2 |
| x2-4 |
分析:(1)方程两边同乘以(x+1)(x-1),化为整式方程求解即可;
(2)根据零指数幂、负整数指数幂、绝对值3个知识点进行计算即可;
(3)先化简,再代入使分母不为0的值代入即可.
(2)根据零指数幂、负整数指数幂、绝对值3个知识点进行计算即可;
(3)先化简,再代入使分母不为0的值代入即可.
解答:解:(1)方程两边同乘以(x+1)(x-1),
得x+1+2x(x-1)=2(x+1)(x-1),
解得x=3,
检验:把x=3代入(x+1)(x-1)=8≠0,
故x=3是原方程的解;
(2)原式=-8+1-8
=-15;
(3)原式=
×
=
,
∵x≠0,2,-2,
∴取x=1代入原式=
=3.
得x+1+2x(x-1)=2(x+1)(x-1),
解得x=3,
检验:把x=3代入(x+1)(x-1)=8≠0,
故x=3是原方程的解;
(2)原式=-8+1-8
=-15;
(3)原式=
| x+2-x |
| x(x-2) |
| (x+2)(x-2) |
| 2 |
=
| x+2 |
| x |
∵x≠0,2,-2,
∴取x=1代入原式=
| 1+2 |
| 1 |
点评:本题考查了分式的化简求值,实数的运算以及解分式方程,是基础知识要熟练掌握.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 )-(-2)3
)-(-2)3
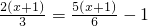 .
.