题目内容
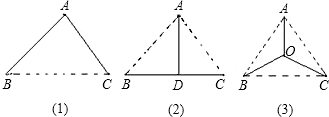
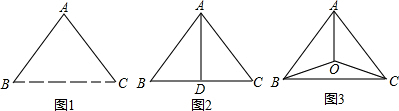
由于水资源缺乏，B，C两地不得不从黄河上的扬水站A处引水，这就需要在A，B，C之间铺设地下输水管道．有人设计了3种铺设方案（图中实线表示管道铺设线路）．在图（2）中，AD⊥BC于点D，且BC=DC；在图（3）中，OA=OB=OC，且AO的延长线交BC于点E，AE⊥BC，BE=EC，OE=
OB．为减少渗漏，节约水资源，并降低工程造价，铺设线路应尽量缩短．若△ABC恰好是一个边长为a的等边三角形，请你通过计算，判断哪一个铺设方案最好．
| 1 | 2 |
分析：根据题目所给的已知条件，利用勾股定理的知识，分别求出第（1）、（2）、（3）种方案铺设路线的长度为2a、a+
a、
a，然后比较大小，找出线路最短的方案即可．
| ||
| 2 |
| 3 |
解答：解：图（1）中，管道长为2a；
图（2）中，AD=
=
=
a，
则管道长为a+
a；
图（3）中，设OE=x，则OB为2x，
由勾股定理得（2x）2-x2=（
a）2，
解得：x=
a，
则OB=
a，管道长为
a×3=
a，
∵2a＞a+
a＞
a，
∴图（3）的辅助设方案最好．
图（2）中，AD=
| AB2-BD2 |
a2-(
|
| ||
| 2 |
则管道长为a+
| ||
| 2 |
图（3）中，设OE=x，则OB为2x，
由勾股定理得（2x）2-x2=（
| 1 |
| 2 |
解得：x=
| ||
| 6 |
则OB=
| ||
| 3 |
| ||
| 3 |
| 3 |
∵2a＞a+
| ||
| 2 |
| 3 |
∴图（3）的辅助设方案最好．
点评：本题考查了勾股定理的应用，解答本题的关键是仔细审题，利用勾股定理计算出有关线段的长度，表示出每种情况下的管道长．
练习册系列答案
阅读快车系列答案
相关题目
．为减少渗漏，节约水资源，并降低工程造价，铺设线路应尽量缩短．若△ABC恰好是一个边长为a的等边三角形，请你通过计算，判断哪一个铺设方案最好．