题目内容
由于水资源缺乏,B,C两地不得不从A地引水,这就需要在A,B,C三地之间铺设地下输水管道.现有三种设计方案:如图,图中实线表示管道铺设线路,在图(2)中,AD⊥BC于点D:在图(3)中,OA=OB=OC.若△ABC是边长为a的等边三角形,为使铺设线路最短,哪种方案最好?(| 2 |
| 3 |
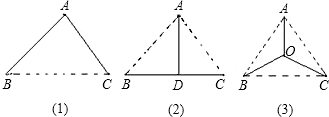
分析:图(1)中,水管的长即为AB+AC=2a;
图(2)中,水管的长即为AD+BC,根据勾股定理和等边三角形的性质求得AD的长即可;
图(3)中,点O是等边三角形的外心,则OA=OB=OC=
AD.
图(2)中,水管的长即为AD+BC,根据勾股定理和等边三角形的性质求得AD的长即可;
图(3)中,点O是等边三角形的外心,则OA=OB=OC=
| 2 |
| 3 |
解答:解:图(1)水管总长:2a;
图(2)水管总长:
a≈1.866a;
图(3)水管总长:
a≈1.732a;
所以图(3)最短,方案(3)好.
图(2)水管总长:
2+
| ||
| 2 |
图(3)水管总长:
| 3 |
所以图(3)最短,方案(3)好.
点评:此题综合运用了等边三角形的性质和勾股定理.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目


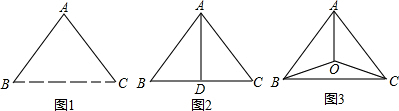
 .为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短.若△ABC恰好是一个边长为a的等边三角形,请你通过计算,判断哪一个铺设方案最好.
.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短.若△ABC恰好是一个边长为a的等边三角形,请你通过计算,判断哪一个铺设方案最好.