题目内容
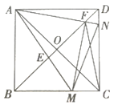
【题目】如图,正方形ABCD的对角线相交于O.点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于E,F两点,且∠MAN=45°,则下列结论:①MN=BM+DN;②△AEF∽△BEM;③
;④△FMC是等腰三角形.其中正确的有（ ）
A.1个B.2个C.3个D.4个
【答案】D
【解析】
将△ABM绕点A逆时针旋转90°至△ADM′，根据正方形的性质和且∠MAN=45°可证明MN=BM+DN；根据三角形的内角和得到∠M′+∠AFD=180°，得到∠AFE=∠M′，推出∠AMB=∠AFE，于是得到△AEF∽△BEM，故②正确；根据相似三角形的判定定理得到△AEB∽△FEM，根据相似三角形的性质得到∠EMF=∠ABE=45°，推出△AFM是等腰直角三角形，于是得到
；故③正确；根据全等三角形的性质得到AF=CF，等量代换得到△FMC是等腰三角形，故④正确．
解：将△ABM绕点A逆时针旋转90°至△ADM′，
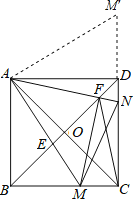
∵∠M′AN=∠DAN+∠MAB=45°，AM′=AM，BM=DM′，
∵∠M′AN=∠MAN=45°，AN=AN，
∴△AMN≌△AM′N′（SAS），
∴MN=NM′，
∴M′N=M′D+DN=BM+DN，
∴MN=BM+DN；故①正确；
∵∠FDM′=135°，∠M′AN=45°，
∴∠M′+∠AFD=180°，
∵∠AFE+∠AFD=180°，
∴∠AFE=∠M′，
∵∠AMB=∠M′，
∴∠AMB=∠AFE，
∵∠EAF=∠EBM=45°，
∴△AEF∽△BEM，故②正确；
∴
，即
，
∵∠AEB=∠MEF，
∴△AEB∽△FEM，
∴∠EMF=∠ABE=45°，
∴△AFM是等腰直角三角形，
∴；故③正确；
在△ADF与△CDF中，
，
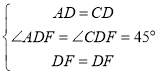∴△ADF≌△CDF（SAS），
∴AF=CF，
∵AF=MF，
∴FM=FC，
∴△FMC是等腰三角形，故④正确；
故选：D．
