题目内容
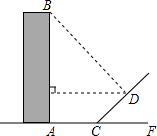 (2013•太原二模)某一时刻,一建筑物的影子恰好落在水平地面和一斜坡上,如图所示,此时测得地面上的影长AC为15米,坡面上的影长CD为10米.已知斜坡的坡角(即∠DCF)为45°,在点D处观测该建筑物顶部点B的仰角(即∠BDE)也恰好为45°,点A,B,C,D在同一平面内,此建筑物的高AB为( )
(2013•太原二模)某一时刻,一建筑物的影子恰好落在水平地面和一斜坡上,如图所示,此时测得地面上的影长AC为15米,坡面上的影长CD为10米.已知斜坡的坡角(即∠DCF)为45°,在点D处观测该建筑物顶部点B的仰角(即∠BDE)也恰好为45°,点A,B,C,D在同一平面内,此建筑物的高AB为( )分析:首先过点D作DH⊥AC于点H,则可得四边形AHDE是矩形,由∠DCF=45°,CD=10米,可得DH=CH=CD•sin45°,继而可求得DE与AE的长,又由∠BDE=45°,即可求得BE的长,继而求得答案.
解答: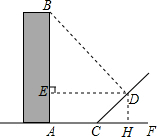 解:如图,过点D作DH⊥AC于点H,
解:如图,过点D作DH⊥AC于点H,
∴四边形AHDE是矩形,
∵∠DCF=45°,CD=10米,
∴DH=CH=CD•sin45°=5
(米),
∴DE=AH=AC+CH=15+5
(米),AE=DH=5
(米),
∵∠BDE=45°,
∴BE=DE=15+5
(米),
∴AB=BE+AE=15+10
(米).
故选D.
 解:如图,过点D作DH⊥AC于点H,
解:如图,过点D作DH⊥AC于点H,∴四边形AHDE是矩形,
∵∠DCF=45°,CD=10米,
∴DH=CH=CD•sin45°=5
| 2 |
∴DE=AH=AC+CH=15+5
| 2 |
| 2 |
∵∠BDE=45°,
∴BE=DE=15+5
| 2 |
∴AB=BE+AE=15+10
| 2 |
故选D.
点评:此题考查了坡度坡角问题以及仰角与俯角问题.此题难度适中,注意能借助于已知构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
相关题目
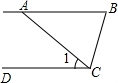 (2013•太原二模)如图,AB∥CD,AC=AB,∠1=40°,则∠B的度数是( )
(2013•太原二模)如图,AB∥CD,AC=AB,∠1=40°,则∠B的度数是( )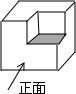 (2013•太原二模)如图的几何体是由一个正方体切去一个小正方体形成的,它的左视图是( )
(2013•太原二模)如图的几何体是由一个正方体切去一个小正方体形成的,它的左视图是( )