题目内容
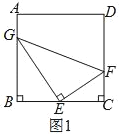
【题目】如图1，正方形ABCD的边长为4，把三角板的直角顶点放置BC中点E处，三角板绕点E旋转，三角板的两边分别交边AB、CD于点G、F．
（1）求证：△GBE∽△GEF．
（2）设AG=x，GF=y，求Y关于X的函数表达式，并写出自变量取值范围．
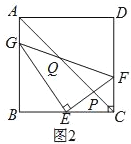
（3）如图2，连接AC交GF于点Q，交EF于点P．当△AGQ与△CEP相似，求线段AG的长．
【答案】（1）见解析；（2）y=4﹣x+
（0≤x≤3）；（3）当△AGQ与△CEP相似，线段AG的长为2或4﹣
．
【解析】
（1）先判断出△BEF'≌△CEF，得出BF'=CF，EF'=EF，进而得出∠BGE=∠EGF，即可得出结论；
（2）先判断出△BEG∽△CFE进而得出CF=
，即可得出结论；
（3）分两种情况，①△AGQ∽△CEP时，判断出∠BGE=60°，即可求出BG；
②△AGQ∽△CPE时，判断出EG∥AC，进而得出△BEG∽△BCA即可得出BG，即可得出结论．
（1）如图1，延长FE交AB的延长线于F'，
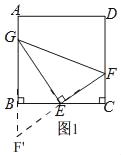
∵点E是BC的中点，
∴BE=CE=2，
∵四边形ABCD是正方形，
∴AB∥CD，
∴∠F'=∠CFE，
在△BEF'和△CEF中，
，
∴△BEF'≌△CEF，
∴BF'=CF，EF'=EF，
∵∠GEF=90°，
∴GF'=GF，
∴∠BGE=∠EGF，
∵∠GBE=∠GEF=90°，
∴△GBE∽△GEF；
（2）∵∠FEG=90°，
∴∠BEG+∠CEF=90°，
∵∠BEG+∠BGE=90°，
∴∠BGE=∠CEF，
∵∠EBG=∠C=90°，
∴△BEG∽△CFE，
∴
，
由（1）知，BE=CE=2，
∵AG=x，
∴BG=4﹣x，
∴
，
∴CF=，
由（1）知，BF'=CF=，
由（1）知，GF'=GF=y，
∴y=GF'=BG+BF'=4﹣x+
当CF=4时，即：=4，
∴x=3，（0≤x≤3），
即：y关于x的函数表达式为y=4﹣x+（0≤x≤3）；
（3）∵AC是正方形ABCD的对角线，
∴∠BAC=∠BCA=45°，
∵△AGQ与△CEP相似，
∴①△AGQ∽△CEP，
∴∠AGQ=∠CEP，
由（2）知，∠CEP=∠BGE，
∴∠AGQ=∠BGE，
由（1）知，∠BGE=∠FGE，
∴∠AGQ=∠BGQ=∠FGE，
∴∠AGQ+∠BGQ+∠FGE=180°，
∴∠BGE=60°，
∴∠BEG=30°，
在Rt△BEG中，BE=2，
∴BG=
，
∴AG=AB﹣BG=4﹣，
②△AGQ∽△CPE，
∴∠AQG=∠CEP，
∵∠CEP=∠BGE=∠FGE，
∴∠AQG=∠FGE，
∴EG∥AC，
∴△BEG∽△BCA，
∴
，
∴
，
∴BG=2，
∴AG=AB﹣BG=2，
即：当△AGQ与△CEP相似，线段AG的长为2或4﹣．
