题目内容
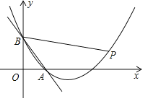
【题目】如图①所示,在三角形纸片![]() 中,
中,![]() ,
,![]() ,将纸片的一角折叠,使点
,将纸片的一角折叠,使点![]() 落在
落在![]() 内的点
内的点![]() 处.
处.
(1)若![]() ,
,![]() ________.
________.
(2)如图①,若各个角度不确定,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系,直接写出结论.
之间的数量关系,直接写出结论.
②当点![]() 落在四边形
落在四边形![]() 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,
外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,![]() ,
,![]() ,
,![]() 之间又存在什么关系?请说明。
之间又存在什么关系?请说明。
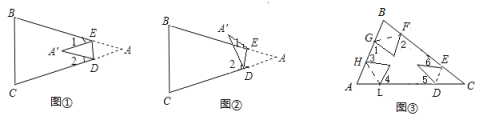
(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的![]() 和是________.
和是________.
【答案】(1)50°;(2)①见解析;②见解析;(3)360°.
【解析】
(1)根据题意,已知![]() ,
,![]() ,可结合三角形内角和定理和折叠变换的性质求解;
,可结合三角形内角和定理和折叠变换的性质求解;
(2)①先根据折叠得:∠ADE=∠A′DE,∠AED=∠A′ED,由两个平角∠AEB和∠ADC得:∠1+∠2等于360°与四个折叠角的差,化简得结果;
②利用两次外角定理得出结论;
(3)由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去(∠B'GF+∠B'FG)以及(∠C'DE+∠C'ED)和(∠A'HL+∠A'LH),再利用三角形的内角和定理即可求解.
解:(1)∵![]() ,
,![]() ,
,
∴∠A′=∠A=180°-(65°+70°)=45°,
∴∠A′ED+∠A′DE =180°-∠A′=135°,
∴∠2=360°-(∠C+∠B+∠1+∠A′ED+∠A′DE)=360°-310°=50°;
(2)①![]() ,理由如下
,理由如下
由折叠得:∠ADE=∠A′DE,∠AED=∠A′ED,
∵∠AEB+∠ADC=360°,
∴∠1+∠2=360°-∠ADE-∠A′DE-∠AED-∠A′ED=360°-2∠ADE-2∠AED,
∴∠1+∠2=2(180°-∠ADE-∠AED)=2∠A;
②![]() ,理由如下:
,理由如下:
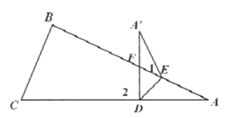
∵![]() 是
是![]() 的一个外角
的一个外角
∴![]() .
.
∵![]() 是
是![]() 的一个外角
的一个外角
∴![]()
又∵![]()
∴![]()
(3)如图
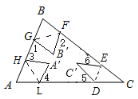
由题意知,
∠1+∠2+∠3+∠4+∠5+∠6=720°-(∠B'GF+∠B'FG)-(∠C'DE+∠C'ED)-(∠A'HL+∠A'LH)=720°-(180°-∠B')-(180°-C')-(180°-A')=180°+(∠B'+∠C'+∠A')
又∵∠B=∠B',∠C=∠C',∠A=∠A',
∠A+∠B+∠C=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°.

【题目】小明和小亮两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
![]() 请计算“
请计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
![]() 一位同学说:“根据实验,一次实验中出现
一位同学说:“根据实验,一次实验中出现![]() 点朝上的概率最大”.这位同学的说法正确吗?为什么?
点朝上的概率最大”.这位同学的说法正确吗?为什么?
![]() 小明和小亮各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为
小明和小亮各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为![]() 的倍数的概率.
的倍数的概率.