题目内容
如图,已知正方形ABCD,将一个45度角∝的顶点放在D点并绕D点旋转,角的两边分别交AB边和BC边于点E和F,连接EF.求证:EF=AE+CF
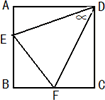
(1)小明是这样思考的:延长BC到G,使得CG=AE,连接DG,先证△DAE≌△DCG,再证△DEF≌△DGF,请你借助下图,按照小明的思路,写出完整的证明思路.

(2)刘老师看到这条题目后,问了小明两个小问题:①如果正方形的边长和△BEF的面积都等于6,求EF的长②将角∝绕D点继续旋转,使得角∝的两边分别和AB边延长线、BC边的延长线交于E和F,如图所示,猜想EF、AE、CF三线段之间的数量关系并给予证明.请你帮忙解决.

答案:
解析:
解析:
|
(1)略 (2)①设EF=x 由(1)知四边形DEBG的面积=正方形ABCD的面积=36,又三角形BEF的面积是6,所以四边形DEFG的面积为30,因为△DAE≌△DCG,EF=FG=x,所以三角形DFG的面积为15,所以1/2·6x=15 解得x=5,所以EF=5 ②如图,延长CF到点G,使得CG=AE,连接DG,易证△DAE≌△DCG所以∠CDG=∠ADE,∵∠ADE+∠CDE=90度,∴∠CDG+∠CDE=90度,∵∠EDF=45度,∴∠GDF=45度,易证△DFE≌△DFG,∴FE=FG,∴CG-CF=FG=EF
∴EF=AE-CF |

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

 如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM.
如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM. (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( )
如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( ) 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.