��Ŀ����
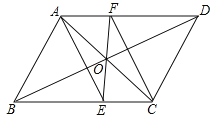
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF������DE������E��EG��DE��ʹEG=DE������FG��FC��
��1�����жϣ�FG��CE��������ϵ�� ��λ�ù�ϵ�� ��
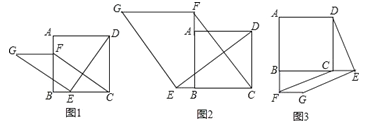
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ�������������жϲ�����֤����
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������ж���
���𰸡���1��FG=CE��FG��CE����2����������3��������
��������
�����������1��ֻҪ֤���ı���CDGF��ƽ���ı��μ��ɵó�FG=CE��FG��CE��
��2�����츨���ߺ�֤����HGE�ա�CED�����ö�Ӧ�������֤�ı���GHBF�Ǿ��κ����õ��������������FG=C��FG��CE��
��3��֤����CBF�ա�DCE����֤���ı���CEGF��ƽ���ı��Σ�
�����������1��FG=CE��FG��CE��
��2������G��GH��CB���ӳ����ڵ�H����EG��DE�����GEH+��DEC=90�㣬�ߡ�GEH+��HGE=90�㣬���DEC=��HGE���ڡ�HGE���CED�У��ߡ�GHE=��DCE����HGE=��DEC��EG=DE�����HGE�ա�CED��AAS������GH=CE��HE=CD����CE=BF����GH=BF����GH��BF�����ı���GHBF�Ǿ��Σ���GF=BH��FG��CH����FG��CE�����ı���ABCD�������Σ���CD=BC����HE=BC����HE+EB=BC+EB����BH=EC����FG=EC��
��3�����ı���ABCD�������Σ���BC=CD����FBC=��ECD=90�㣬�ڡ�CBF���DCE�У���BF=CE����FBC=��ECD��BC=DC�����CBF�ա�DCE��SAS�������BCF=��CDE��CF=DE����EG=DE����CF=EG����DE��EG�����DEC+��CEG=90�����ߡ�CDE+��DEC=90�������CDE=��CEG�����BCF=��CEG����CF��EG�����ı���CEGFƽ���ı��Σ���FG��CE��FG=CE��