题目内容
【题目】如图,AE∥CF,∠A=∠C.
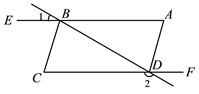
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若AD平分∠BDF,试说明BC平分∠DBE.
【答案】见解析
【解析】试题分析:(1)由平行线的性质求得∠BDC=∠1=35°,然后由邻补角的定义求得∠2的度数即可;
(2)由平行线的性质可知:∠A+∠ADC=180°,然后由∵∠A=∠C,再证得∠C+∠ADC=180°,从而可证得BC∥AD;
(3)由AE∥CF可证明∠BDF=∠DBE,由BC∥AD,可证明∠ADB=∠DBC,由角平分线的定义可知,∠ADB=![]() ∠BDF,从而可证明∠DBC=
∠BDF,从而可证明∠DBC=![]() ∠EBD.
∠EBD.
试题解析:(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°-∠BDC=180°-35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,∴∠A+∠ADC=180°,
又∵∠A=∠C,∴∠C+∠ADC=180°,
∴BC∥AD.
(3)∵AE∥CF,∴∠BDF=∠DBE.
∵BC∥AD,∴∠ADB=∠DBC.
∵AD平分∠BDF,∴∠ADB=![]() ∠BDF,∴∠DBC=
∠BDF,∴∠DBC=![]() ∠EBD.
∠EBD.
∴BC平分∠DBE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目