题目内容
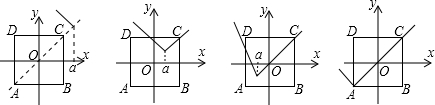
在直角坐标系中,有以A(-1,-1),B(1,-1),C(1,1),D(-1,1)为顶点的正方形,设它在折线y=|x-a|+a上侧部分的面积为S,试求S关于的函数关系式,并画出它们的图象.分析:思路点拨先画出符合题意的图形,然后对不确定折线y=|x-a|+a及其中的字母a的取值范围进行分类讨论,a的取值决定了正方形在折线上侧部分的图形的形状.
解答:解:(1)当a≥1时,y=|x-a|+a的图象与正方形ADCD没有公共部分,S=0;
(2)当0≤a<1时,S=
(1-a)×2(1-a)=(1-a)2;
(3)当-1≤a<0时,S=2-
=2-(1+a)2;
(4)当a<-1时,S=2.
答:S与a的函数关系式为S=
;
函数图象如下图所示:
(2)当0≤a<1时,S=
| 1 |
| 2 |
(3)当-1≤a<0时,S=2-
| 2(1-|a|)(1-|a|) |
| 2 |
(4)当a<-1时,S=2.
答:S与a的函数关系式为S=
|
函数图象如下图所示:

点评:我们把有自变量或关于自变量的代数式包含在绝对值符号在内的一类函数称为绝对值函数.去掉绝对值符号,把绝对值函数化为分段函数,这是解绝对值的一般思路.

练习册系列答案
相关题目
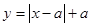 上侧部分的面积为S.当
上侧部分的面积为S.当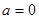 时,S= ▲ ;当
时,S= ▲ ;当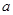 为任意实数时,面积S的最大值为 ▲ .
为任意实数时,面积S的最大值为 ▲ . 时,求S的值;
时,求S的值;