题目内容
如图,已知双曲线 经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为 .
经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为 .
【答案】分析:要求△AOC的面积,已知OB为高,只要求AC长,即点C的坐标即可,由点D为三角形OAB斜边OA的中点,且点A的坐标(-6,4),可得点D的坐标为(-3,2),代入双曲线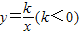 可得k,又AB⊥OB,所以C点的横坐标为-6,代入解析式可得纵坐标,继而可求得面积.
可得k,又AB⊥OB,所以C点的横坐标为-6,代入解析式可得纵坐标,继而可求得面积.
解答:解:∵点D为△OAB斜边OA的中点,且点A的坐标(-6,4),
∴点D的坐标为(-3,2),
把(-3,2)代入双曲线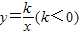 ,
,
可得k=-6,
即双曲线解析式为y=-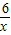 ,
,
∵AB⊥OB,且点A的坐标(-6,4),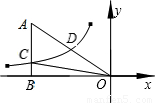
∴C点的横坐标为-6,代入解析式y=-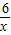 ,
,
y=1,
即点C坐标为(-6,1),
∴AC=3,
又∵OB=6,
∴S△AOC= ×AC×OB=9.
×AC×OB=9.
故答案为:9.
点评:本题考查反比例函数系数k的几何意义及其函数图象上点的坐标特征,体现了数形结合的思想.
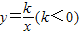 可得k,又AB⊥OB,所以C点的横坐标为-6,代入解析式可得纵坐标,继而可求得面积.
可得k,又AB⊥OB,所以C点的横坐标为-6,代入解析式可得纵坐标,继而可求得面积.解答:解:∵点D为△OAB斜边OA的中点,且点A的坐标(-6,4),
∴点D的坐标为(-3,2),
把(-3,2)代入双曲线
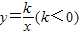 ,
,可得k=-6,
即双曲线解析式为y=-
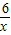 ,
,∵AB⊥OB,且点A的坐标(-6,4),

∴C点的横坐标为-6,代入解析式y=-
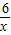 ,
,y=1,
即点C坐标为(-6,1),
∴AC=3,
又∵OB=6,
∴S△AOC=
 ×AC×OB=9.
×AC×OB=9.故答案为:9.
点评:本题考查反比例函数系数k的几何意义及其函数图象上点的坐标特征,体现了数形结合的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(
经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为( ,4),则△AOC的面积为(
)
,4),则△AOC的面积为(
) 
 经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为6,则
经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为6,则 =_________.
=_________.