Question

【题目】如图,△ABC是圆O的内接三角形,∠BAD是△ABC的一个外角,∠BAC,∠BAD的平分线分别交圆O于点E、F.若连接EF则EF与BC有怎样的位置关系?为什么?

Answer 1

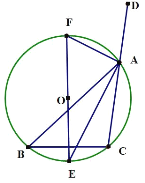
【答案】垂直平分；理由见解析

【解析】

试题分析：根据外角的平分线和内角的平分线得出∠FAE是直角，从而得出EF为直径，根据角平分线得出点E是弧BC的中点，从而根据垂径定理的逆定理得出关系.

试题解析：根据三角形外角的性质可得：∠BAD=∠B+∠C ∵AF平分∠BAD，AE平分∠BAC

∴∠FAB=(∠B+∠C) ∠BAE=∠BAC ∴∠FAE=(∠B+∠C+∠BAC)=×180°=90°

∴EF是直径 ∵AE平分∠BAC ∴点E是弧BC的中点 ∴EF垂直平分BC