题目内容
【题目】如图所示,是某市一条高速公路上的隧道口在平面直角坐标系上的示意图，路面OA宽8m,P处有一照明灯，从O、A两处观测P处，仰角分别为
、
，且
。以O为原点，OA所在直线为x轴建立直角坐标系。
（1）求P点坐标。
（2）现有一辆货车，宽为4 m，高为2.5m，它能否安全通过这个隧道？说明理由。
【答案】(1)P(6,3) ；(2)y=-
；可以通过.
【解析】试题分析：(1)过点P作PC 
，根据
得出 OC＝2PC，AC＝
，再根据OA＝OC+CA和OA＝8得出PC＝3、OC＝6、CA＝2，即可写出点P的坐标；
（2）设二次函数的解析式为y=ax2+bx+c，将O、A、P的坐标代入函数解析中，即可求得二次函数的解析式，当 x=6时，y=3>2.5即可通过.
试题解析：
(1)过点P作PC 
，如图的示：
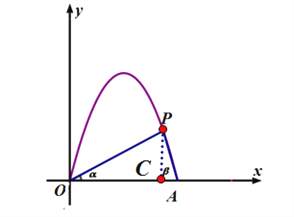
∵△OPC和△PAC是直角三角形， 
∴
，
∴OC＝2PC，AC＝
，
∵OA＝OC+CA，OA＝8，
∴
，
∴PC＝3，
∴OC＝6，CA＝2，
∴点P的坐标为（6，3）.
(2)设隧道口的函数解析式为：y=ax2+bx+c
∵点A（8，0）、O（0，0）、P（6，3）在函数的图像上，
∴
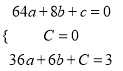
解得：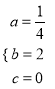 
所以函数解析式为：y=-1/4
当x=6时，y=3>2.5,
可以通过.
练习册系列答案
相关题目
