题目内容
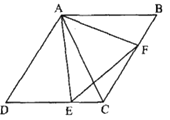
【题目】如图，AD是△ABC的中线，E、F分别是AD和AD延长线上的点，且DE=DF，连结BF，CE．下列说法：①△ABD和△ACD面积相等；②CE=AE；③△BDF≌△CDE； ④BF∥CE；⑤∠BAD=∠CAD．其中正确的有( ).
A.①⑤B.③⑤C.①③④D.①②④
【答案】C
【解析】
由等底同高的三角形面积相等可判断①，无法得出CE=AE，故②错误，利用SAS易证△BDF≌△CDE，可知③正确，由△BDF≌△CDE的对应角相等，利用内错角相等两直线平行可判断④，因题目条件没有AB=AC，无法得到∠BAD=∠CAD，故⑤错误.
解：∵AD是△ABC的中线
∴BD=CD
∴△ABD和△ACD面积相等，故①正确；
无法得出CE=AE，故②错误；
在△BDF和△CDE中，
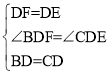
∴BDF≌△CDE（SAS），故③正确；
∵BDF≌△CDE
∴∠F=∠CED
∴BF∥CE，故④正确；
因题目条件没有AB=AC，无法用等腰三角形三线合一得到∠BAD=∠CAD，故⑤错误.
①③④正确，故选C.
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
