ЬтФПФкШн
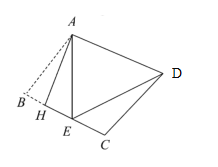
ЁОЬтФПЁПШчЭМЃЌбЇаЃЕФВйГЁЩЯгавЛЦьИЫABЃЌМздкВйГЁЩЯЕФCДІЪњСЂ3 mИпЕФжёИЭCDЃЛввДгCДІЭЫЕНEДІЧЁКУПДЕНжёИЭЖЅЖЫDгыЦьИЫЖЅЖЫBжиКЯЃЌСПЕУCEЃН3 mЃЌввЕФблОІЕНЕиУцЕФОрРыFEЃН1.5 mЃЛБћдкC1ДІЪњСЂ3 mИпЕФжёИЭC1D1ЃЌввДгEДІКѓЭЫ6 mЕНE1ДІЃЌЧЁКУПДЕНСНИљжёИЭКЭЦьИЫжиКЯЃЌЧвжёИЭЖЅЖЫD1гыЦьИЫЖЅЖЫBвВжиКЯЃЌСПЕУC1E1ЃН4 mЃЎЧѓЦьИЫABЕФИпЃЎ
ЁОД№АИЁП10.5m.
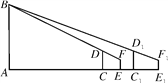
ЁОНтЮіЁПЪдЬтЗжЮіЃКШчЭМЃЌСЌНгF1FЃЌВЂбгГЄЪЙжЎгыABЯрНЛЃЌЩшЦфгыABЃЌCDЃЌC1D1ЗжБ№НЛгкЕуGЃЌMЃЌNЃЌЩшBGЃНx mЃЌGMЃНy m. ИљОнЬтвтЗжБ№ЧѓДІDMЁЂFGЁЂFMЁЂND1ЁЂF1NЁЂF1GЕФГЄЖШЃЌИљОнШ§НЧаЮЯрЫЦСаЗНГЬзщЃЌНтЗНГЬзщМДПЩ.
ЪдЬтНтЮіЃК

ШчЭМЃЌСЌНгF1FЃЌВЂбгГЄЪЙжЎгыABЯрНЛЃЌЩшЦфгыABЃЌCDЃЌC1D1ЗжБ№НЛгкЕуGЃЌMЃЌNЃЌЩшBGЃНxmЃЌGMЃНym.
ЁрDM=1.5mЃЌFG=ЃЈy+3ЃЉmЃЌFM=3mЃЌND1=1.5mЃЌF1N=4mЃЌF1G=ЃЈy+6+3ЃЉmЃЌ
ЁпDMЁЮBGЃЌЁрЁїFDMЁзЁїFBG.
Ёр![]() =
=![]() ЃЌдђ
ЃЌдђ![]() =
=![]() ЂйЃЛ
ЂйЃЛ
гжЁпND1ЁЮGBЃЌЁрЁїF1D1NЁзЁїF1BG.
Ёр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЂкЃЛ
ЂкЃЛ
СЊСЂЂйЂкЃЌНтЗНГЬзщЃЌЕУ![]() ЃЌ
ЃЌ
ЙЪЦьИЫABЕФИпЮЊ9ЃЋ1.5ЃН10.5(m)ЃЎ