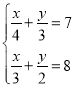题目内容
【题目】如图，在正三角形ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，FD⊥BC，则△DEF的面积与△ABC的面积之比等于 ．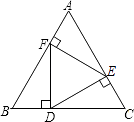 
【答案】1：3
【解析】解：∵△ABC是正三角形，
∴∠B=∠C=∠A=60°，
∵DE⊥AC，EF⊥AB，FD⊥BC，
∴∠AFE=∠CED=∠BDF=90°，
∴∠BFD=∠CDE=∠AEF=30°，
∴∠DFE=∠FED=∠EDF=60°， 
，
∴△DEF是正三角形，
∴BD：DF=1： 
①，BD：AB=1：3②，△DEF∽△ABC，
①÷②， 
= ，
∴DF：AB=1： ，
∴△DEF的面积与△ABC的面积之比等于1：3．
所以答案是：1：3．
【考点精析】认真审题，首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)，还要掌握含30度角的直角三角形(在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
