题目内容
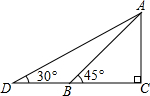 (2013•保康县二模)如图,某幼儿园为了加强安全管理,决定将幼儿园内的滑梯的倾角由45°改为30°,已知原滑梯AB的长为5米,在高度不变的情况下,新滑梯长为AD,点D、B、C 在同一水平地面上.
(2013•保康县二模)如图,某幼儿园为了加强安全管理,决定将幼儿园内的滑梯的倾角由45°改为30°,已知原滑梯AB的长为5米,在高度不变的情况下,新滑梯长为AD,点D、B、C 在同一水平地面上.(1)改善后滑梯会加长多少?(精确到0.01)
(2)若滑梯的正前方能有3米长的空地就能保证安全,若原滑梯的前方有6米长的空地,像这样改造是否可行?说明理由.(参考数据:
| 2 |
| 3 |
| 6 |
分析:本题中两个直角三角形有公共的边,那么可利用这条公共直角边进行求解.
(1)求AD长的时候,可在直角三角形ADC内,根据∠D的度数和AC的长,运用正弦函数求出AD的长.
(2)本题实际要求的是BD的长是否超过3m,如果超过了那么这样修改滑板的坡度就不可行,反之,则可行.就要先求出BD的长.根据BD=CD-BC即可求解.
(1)求AD长的时候,可在直角三角形ADC内,根据∠D的度数和AC的长,运用正弦函数求出AD的长.
(2)本题实际要求的是BD的长是否超过3m,如果超过了那么这样修改滑板的坡度就不可行,反之,则可行.就要先求出BD的长.根据BD=CD-BC即可求解.
解答:解:(1)Rt△ABC中,AC=AB×sin45°=
(m)
Rt△ADC中,BC=AB×cos45°=
(m),
AD=
=5
∴AD-AB≈2.07(m).
改善后的滑梯会加长2.07 m;
(2)这样改造能行.
因为CD-BC≈2.59(m),而6-3>2.59.
5
| ||
| 2 |
Rt△ADC中,BC=AB×cos45°=
5
| ||
| 2 |
AD=
| AC |
| sin300 |
| 2 |
∴AD-AB≈2.07(m).
改善后的滑梯会加长2.07 m;
(2)这样改造能行.
因为CD-BC≈2.59(m),而6-3>2.59.
点评:本题主要考查了解直角三角形的应用,利用这两个直角三角形有公共的直角边求解是解决此类题目的基本出发点.

练习册系列答案
相关题目
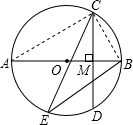 (2013•保康县二模)如图,在⊙O中,AB为直径,弦CD⊥直径AB于点M.
(2013•保康县二模)如图,在⊙O中,AB为直径,弦CD⊥直径AB于点M.