题目内容
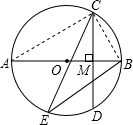 (2013•保康县二模)如图,在⊙O中,AB为直径,弦CD⊥直径AB于点M.
(2013•保康县二模)如图,在⊙O中,AB为直径,弦CD⊥直径AB于点M.(1)若CE为∠ACB的平分线,交⊙O于点E,求∠ABE的度数.
(2)若AM=18,BM=8.求弦CD的长.
分析:(1)根据圆周角定理讨论得到∠ACB=90°,由CE为∠ACB的平分线,则∠ACE=
∠ACB=45°,然后根据圆周角定理得到∠ABE=∠ACE=45°;
(2)由CD⊥AB,根据垂径定理得到CM=DM,∠AMC=∠BMC=90°,根据等角的余角相等得到∠A=∠BCM,根据相似的判定方法得到Rt△ACM∽Rt△CBM,利用相似比得到CM2=AB•BM,可计算出CM=12,所以CD=2CM=24.
| 1 |
| 2 |
(2)由CD⊥AB,根据垂径定理得到CM=DM,∠AMC=∠BMC=90°,根据等角的余角相等得到∠A=∠BCM,根据相似的判定方法得到Rt△ACM∽Rt△CBM,利用相似比得到CM2=AB•BM,可计算出CM=12,所以CD=2CM=24.
解答:解:(1)∵AB为圆O的直径,
∴∠ACB=90°,
∵CE为∠ACB的平分线,
∴∠ACE=
∠ACB=45°,
∴∠ABE=∠ACE=45°;
(2)∵CD⊥AB,
∴CM=DM,∠AMC=∠BMC=90°,
∵∠ACB=90°,
∴∠A+∠ACM=∠ACM+∠BCM=90°,
∴∠A=∠BCM,
∴Rt△ACM∽Rt△CBM,
∴
=
,即CM2=AB•BM,
∵AM=18,BM=8,
∴CM2=18×8,
∴CM=12,
∴CD=2CM=24.
∴∠ACB=90°,
∵CE为∠ACB的平分线,
∴∠ACE=
| 1 |
| 2 |
∴∠ABE=∠ACE=45°;
(2)∵CD⊥AB,
∴CM=DM,∠AMC=∠BMC=90°,
∵∠ACB=90°,
∴∠A+∠ACM=∠ACM+∠BCM=90°,
∴∠A=∠BCM,
∴Rt△ACM∽Rt△CBM,
∴
| AM |
| CM |
| CM |
| BM |
∵AM=18,BM=8,
∴CM2=18×8,
∴CM=12,
∴CD=2CM=24.
点评:本题考查了相似三角形的判定与性质:有两组角分别相等的两个三角形相似;相似三角形的对应角相等,对应边的比相等.也考查了垂径定理和圆周角定理.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目