题目内容
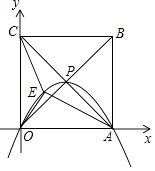
【题目】如图，已知点 A（-1,0）和点B（1,2） ，在 y 轴正半轴上确定点 P ，使得△ABP 为直角三角形，则满足条件的点 P 的坐标为 ． 
【答案】（0,3）或（0,1+
）.
【解析】①如下图，
过点B作BP⊥AB，交y轴于点P，过点B作BD⊥OP，交OP于点D，
∴∠ABP=90°，BD=1，
∵点 A（-1,0），点B（1,2） 在直线AB上，
∴直线AB的函数解析式为：y=x+1，
∴点C（0，1），
即OC=1=OA，
∴
AOC是等腰三角形，
∴∠ACO=∠BCP=45°，
∴BCP是等腰直角三角形，
∴CP=2BD=2，
∴OP=3，
即点P的坐标为（0，3）.
②如下图：
当∠APB=90°时，
∵点 A（-1,0），点B（1,2），点C（0，1），
∴点C为AB的中点，AB=
，
∴CP=
AB=，
∴OP=1+，
∴点P（0，1+），
综上，点P的坐标为（0，3）或（0，1+）.
所以答案是：（0，3）或（0，1+）.
【考点精析】解答此题的关键在于理解勾股定理的逆定理的相关知识，掌握如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．
练习册系列答案
相关题目
【题目】为了创建国家卫生城市，需要购买甲、乙两种类型的分类垃圾桶替换原来的垃圾桶，
，
，
三个小区所购买的数量和总价如表所示．
甲型垃圾桶数量（套） | 乙型垃圾桶数量（套） | 总价（元） | |
|
|
|
|
|
|
|
|
|
|
|
|
（1）问甲型垃圾桶、乙型垃圾桶的单价分别是每套多少元？
（2）求
，
的值．
