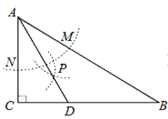
题目内容
【题目】如图所示, ![]() 是
是![]() 的角平分线,以点
的角平分线,以点![]() 为圆心,
为圆心, ![]() 为半径作圆交
为半径作圆交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() .
.
(![]() )求证:
)求证: ![]() ;
;
(![]() )求证:点
)求证:点![]() 是
是![]() 的中点;
的中点;
(![]() )如果
)如果![]() ,求半径
,求半径![]() 的长.
的长.

【答案】(1)见解析;(2)见解析;(3)5.
【解析】试题分析:(1)由直径所对的圆周角等于![]() ,即可得证;
,即可得证;
(2)由AD是△ABC的角平分线,∠B=∠CAE,易证得∠ADE=∠DAE,即可得ED=EA,又由ED是直径,根据直径所对的圆周角是直角,可得EF⊥AD,由三线合一的知识,即可判定点F是AD的中点;
(3)易证得△AEC∽△BEA,然后由相似三角形的对应边成比例,即可求得答案.
试题解析:(![]() )∵
)∵![]() 是⊙
是⊙![]() 直径,
直径,
∴![]() ,
,
∴![]() .
.
(![]() )∵
)∵![]() 平分
平分![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形,
是等腰三角形,
∵![]() ,
,
∴![]() 是
是![]() 中点(三线合一).
中点(三线合一).
(![]() )设⊙
)设⊙![]() 半径为
半径为![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
∴在![]() 和
和![]() 中
中
![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.