题目内容
已知a+b=3，ab=2，求a2b+ab2，a2+b2的值。
a2b＋ab2= ab(a＋b)
因为a＋b=3，ab=2，
所以，原式==2×3=6
因为a＋b=3，所以(a＋b) 2=9
则a2＋2ab＋b2=9
把ab=2代入得a2＋2×2＋b2=所以a2＋b2=5
（1）把代数式提取公因式ab后把a+b=3，ab=2整体代入求解；
（2）利用完全平方公式把代数式化为已知的形式求解
因为a＋b=3，ab=2，
所以，原式==2×3=6
因为a＋b=3，所以(a＋b) 2=9
则a2＋2ab＋b2=9
把ab=2代入得a2＋2×2＋b2=所以a2＋b2=5
（1）把代数式提取公因式ab后把a+b=3，ab=2整体代入求解；
（2）利用完全平方公式把代数式化为已知的形式求解
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
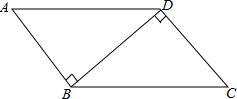已知：如图，AB⊥BD，CD⊥BD，AD=BC．求证：
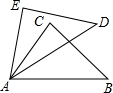如图，已知AE=AC，AD=AB，∠EAD=∠CAB，求证：∠B=∠D．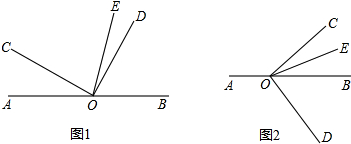
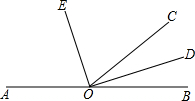如图，已知点O是直线AB上的一点，∠BOC=40°，OD、OE分别是∠BOC、∠AOC的角平分线．