题目内容
【题目】已知:如图,线段AB和射线BM交于点B. 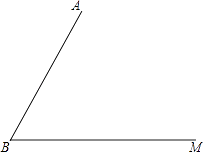
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法).
①在射线BM上作一点C,使AC=AB;
②作∠ABM的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明.
【答案】
(1)解:如图所示:
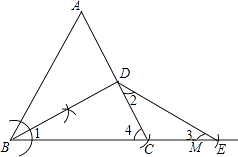
(2)解:BD=DE,
证明:∵BD平分∠ABC,
∴∠1= ![]() ∠ABC.
∠ABC.
∵AB=AC,
∴∠ABC=∠4.
∴∠1= ![]() ∠4.
∠4.
∵CE=CD,
∴∠2=∠3.
∵∠4=∠2+∠3,
∴∠3= ![]() ∠4.
∠4.
∴∠1=∠3.
∴BD=DE
【解析】(1)①以A为圆心,AB长为半径画弧交BC于C;②根据角平分线的作法作∠ABM的角平分线;③以C为圆心CD长为半径画弧交CM于E,再连接ED即可;(2)根据角平分线的性质可得∠1= ![]() ∠ABC,根据等边对等角可得∠ABC=∠4,∠2=∠3,然后再证明∠1=∠3,根据等角对等边可得BD=DE.
∠ABC,根据等边对等角可得∠ABC=∠4,∠2=∠3,然后再证明∠1=∠3,根据等角对等边可得BD=DE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目