题目内容
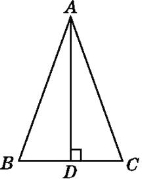
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的一点,过点F 作FG⊥BC于G点,并交AB于E点.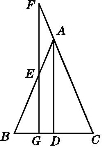
(1)求证:AD∥FG;
(2)△AFE为等腰三角形.
【答案】
(1)证明:∵AB=AC,D是BC的中点,
∴AD⊥BC.
又∵FG⊥BC,
∴AD∥FG .
(2)证明:∵AB=AC,D是BC的中点,
∴∠BAD=∠CAD.
∵AD∥FG,
∴∠F=∠CAD,∠AEF=∠BAD.
∴∠F=∠AEF.
∴AF=AE,
即△AEF是等腰三角形
【解析】(1)根据等腰三角形的三线合一得出AD⊥BC.又FG⊥BC,根据同一平面内垂直于同一直线的两条直线互相平行得出AD∥FG ;
(2)根据等腰三角形的三线合一得出∠BAD=∠CAD,根据二直线平行内错相等,同位角相等得出∠F=∠CAD,∠AEF=∠BAD.从而得出∠F=∠AEF,根据两角相等的三角形是等腰三角形得出结论。
【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案,需要熟知由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
【题目】某校篮球队13名同学的身高如下表:
身高(cm) | 175 | 180 | 182 | 185 | 188 |
人数(个) | 1 | 5 | 4 | 2 | 1 |
则该校篮球队13名同学身高的众数和中位数分别是( )
A.182,180
B.180,180
C.180,182
D.188,182