题目内容
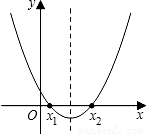
福娃们在一起探讨研究下面的题目:函数y=x2-x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-1时,函数值是多少?贝贝:我注意到当x=0时,y=m>0.
晶晶:我发现图象的对称轴为
 .
.欢欢:我判断出x1<a<x2.
迎迎:我认为关键要判断a-1的符号.
妮妮:M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y}可以取一个特殊的值.
参考上面福娃们的讨论,请你解该题,你选择的答案是( )

A.y<0
B.0<y<m
C.y>m
D.y=m
【答案】分析:把x=a代入函数y=x2-x+m中求出函数a、a-1与0的关系,进而确定x=a-1时,函数y=x2-x+m的值.
解答:解:x=a代入函数y=x2-x+m中得:y=a2-a+m=a(a-1)+m,
∵x=a时,y<0,
∴a(a-1)+m<0,
由图象可知:m>0,
∴a(a-1)<0,
又∵x=a时,y<0,
∴a>0则a-1<0,
由图象可知:x=0时,y=m,
又∵x< 时y随x的增大而减小,
时y随x的增大而减小,
∴x=a-1时,y>m.
故选:C.
点评:此题主要考查了二次函数的性质,利用数形结合法、假设法都是解决数学习题常用的方法,巧妙运用解题方法可以节省解题时间.
解答:解:x=a代入函数y=x2-x+m中得:y=a2-a+m=a(a-1)+m,
∵x=a时,y<0,
∴a(a-1)+m<0,
由图象可知:m>0,
∴a(a-1)<0,
又∵x=a时,y<0,
∴a>0则a-1<0,
由图象可知:x=0时,y=m,
又∵x<
 时y随x的增大而减小,
时y随x的增大而减小,∴x=a-1时,y>m.
故选:C.
点评:此题主要考查了二次函数的性质,利用数形结合法、假设法都是解决数学习题常用的方法,巧妙运用解题方法可以节省解题时间.

练习册系列答案
相关题目
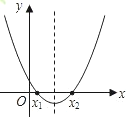 福娃们在一起探讨研究下面的题目:函数y=x2-x+m(m为常数)的图象如下图,如果x=a时,y<0;那么x=a-1时,函数值是多少.参考下面福娃们的讨论,请你解该题,你选择的答案是( )
福娃们在一起探讨研究下面的题目:函数y=x2-x+m(m为常数)的图象如下图,如果x=a时,y<0;那么x=a-1时,函数值是多少.参考下面福娃们的讨论,请你解该题,你选择的答案是( )
| A、y<0 | B、0<y<m | C、y>m | D、y=m |
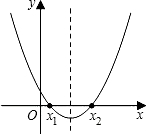 a-1时,函数值( )
a-1时,函数值( ) ;那么x=a-1时,函数值是多少?
;那么x=a-1时,函数值是多少?


 .
.