��Ŀ����
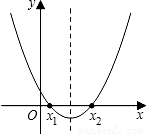
��������һ��̽���о�������y=x2-x+m��mΪ��������ͼ����ͼ�����x=aʱ��y��0����ôx=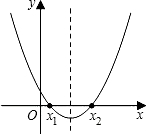 a-1ʱ������ֵ��������
a-1ʱ������ֵ��������
�ο����渣���ǵ����ۣ��������⣬��ѡ��Ĵ��ǣ�������
��������ע���x=0ʱ��y=m��0��
�������ҷ���ͼ��ĶԳ���Ϊx=
��
���������жϳ�x1��a��x2��
ӭӭ������Ϊ�ؼ�Ҫ�ж�a-1�ķ��ţ�
���ݣ�m����ȡһ�������ֵ��
 a-1ʱ������ֵ��������
a-1ʱ������ֵ���������ο����渣���ǵ����ۣ��������⣬��ѡ��Ĵ��ǣ�������
��������ע���x=0ʱ��y=m��0��
�������ҷ���ͼ��ĶԳ���Ϊx=
| 1 |
| 2 |
���������жϳ�x1��a��x2��
ӭӭ������Ϊ�ؼ�Ҫ�ж�a-1�ķ��ţ�
���ݣ�m����ȡһ�������ֵ��
| A��y��0 | B��0��y��m |
| C��y��m | D��y=m |
��������������ϵ�ж������ķ�Χ������x1��a��x2����ȷ��a�ķ�Χ����֪x=a-1�ķ��ţ��Ӷ�ȷ����Ӧ�ĺ���ֵ�ķ��ţ�
����⣺��������ϵ��֪��x1+x2=1��x1•x2=m��0��
��0��x1��x2��1��
�֡�x1��a��x2��1��
��x=a-1��0��x=0ʱ��y=m��
��x��
ʱ��y��x���������С��
�൱x=a-1ʱ��y��m����ѡC��
��0��x1��x2��1��
�֡�x1��a��x2��1��
��x=a-1��0��x=0ʱ��y=m��
��x��
| 1 |
| 2 |
�൱x=a-1ʱ��y��m����ѡC��
���������⿼����������ϵ�����������Ե����ã�

��ϰ��ϵ�д�
�����Ŀ
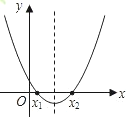 ��������һ��̽���о��������Ŀ������y=x2-x+m��mΪ��������ͼ������ͼ�����x=aʱ��y��0����ôx=a-1ʱ������ֵ�Ƕ��٣��ο����渣���ǵ����ۣ��������⣬��ѡ��Ĵ��ǣ�������
��������һ��̽���о��������Ŀ������y=x2-x+m��mΪ��������ͼ������ͼ�����x=aʱ��y��0����ôx=a-1ʱ������ֵ�Ƕ��٣��ο����渣���ǵ����ۣ��������⣬��ѡ��Ĵ��ǣ�������
 ����ôx=a-1ʱ������ֵ�Ƕ��٣�
����ôx=a-1ʱ������ֵ�Ƕ��٣�


 ��
��