题目内容
【题目】在△ABC中,AB=AC,D为射线BA上一点,连接DC,且DC=BC.
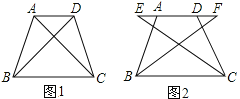
(1)如图1,若DC⊥AC,AB=![]() ,求CD的长;
,求CD的长;
(2)如图2,若E为AC上一点,且CE=AD;连接BE,BE=2CE,连接DE并延长交BC于F.求证:DF=3EF.

【答案】(1)CD=![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】分析:(1)由AB=AC,DC=BC,可得出∠1=∠2=∠3=30°,利用特殊三角函数值即可求解;(2)过A作AH⊥DF于H,利用![]() 和
和![]() 可得结果.
可得结果.
本题解析:
解∵AB=AC,BC=DC∴∠1=∠2,∠1=∠3 ∴∠2=∠3 又∵DC⊥AC ∴∠ACD=900∴∠1+∠2+∠3=900 ∴∠1=∠2=∠3=300
∵AB=![]() ∴AC=
∴AC=![]() ∴CD=
∴CD=![]()


②证明:∵AB=AC,BC=DC∴∠ABC=∠ACB,∠ABC=∠CDA
∴∠BCE=∠CDA 又∵BC=DC,CE=DA ∴![]() ∴CE=AD,BE=AC
∴CE=AD,BE=AC
又∵BE=2CE ∴AE=CE,AD=AE ,过A作AH⊥DF于H,则∠DAH=∠HAE,DH=EH, 又∵∠DAC=∠ABC+∠ACB=2∠ACB ,∴∠HAE=∠ACB ,又∵∠AEH=∠CEF,AE=CE∴![]() ∴EH=EF ,∴DH=EH=EF,即DF=3EF
∴EH=EF ,∴DH=EH=EF,即DF=3EF

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目