题目内容
一个三角形三边长分别为5,12,13,R是其外接圆半径,r是其内切圆半径,则R-r 的值
- A.4.5
- B.3.5
- C.5.5
- D.2.5
A
分析:根据勾股定理的逆定理推出∠C=90°,连接OE、OQ,根据圆O是三角形ABC的内切圆,得到AE=AF,BQ=BF,∠OEC=∠OQC=90°,OE=OQ,推出正方形OECQ,设OE=CE=CQ=OQ=r,得到方程12-r+5-r=13,求出方程的解即可,进而得出其外接圆半径,即可得出答案.
解答: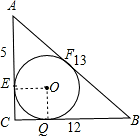 解:∵AC2+BC2=25+144=169,AB2=169,
解:∵AC2+BC2=25+144=169,AB2=169,
∴AC2+BC2=AB2,
∴∠C=90°,
连接OE、OQ,
∵圆O是三角形ABC的内切圆,
∴AE=AF,BQ=BF,∠OEC=∠OQC=∠C=90°,OE=OQ,
∴四边形OECQ是正方形,
∴设OE=CE=CQ=OQ=r,
∵AF+BF=13,
∴12-r+5-r=13,
∴r=2,
∵直角三角形斜边长是直角三角形外接圆直径,
∴其外接圆半径为:R=6.5,
∴R-r=6.5-2=4.5.
故选:A.
点评:此题主要考查了对三角形的内切圆与内心以及直角三角形外接圆半径求法、切线长定理,切线的性质,正方形的性质和判定,勾股定理的逆定理等知识点,综合运用这些性质进行推理是解此题的关键.题型较好,综合性强.
分析:根据勾股定理的逆定理推出∠C=90°,连接OE、OQ,根据圆O是三角形ABC的内切圆,得到AE=AF,BQ=BF,∠OEC=∠OQC=90°,OE=OQ,推出正方形OECQ,设OE=CE=CQ=OQ=r,得到方程12-r+5-r=13,求出方程的解即可,进而得出其外接圆半径,即可得出答案.
解答:
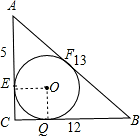 解:∵AC2+BC2=25+144=169,AB2=169,
解:∵AC2+BC2=25+144=169,AB2=169,∴AC2+BC2=AB2,
∴∠C=90°,
连接OE、OQ,
∵圆O是三角形ABC的内切圆,
∴AE=AF,BQ=BF,∠OEC=∠OQC=∠C=90°,OE=OQ,
∴四边形OECQ是正方形,
∴设OE=CE=CQ=OQ=r,
∵AF+BF=13,
∴12-r+5-r=13,
∴r=2,
∵直角三角形斜边长是直角三角形外接圆直径,
∴其外接圆半径为:R=6.5,
∴R-r=6.5-2=4.5.
故选:A.
点评:此题主要考查了对三角形的内切圆与内心以及直角三角形外接圆半径求法、切线长定理,切线的性质,正方形的性质和判定,勾股定理的逆定理等知识点,综合运用这些性质进行推理是解此题的关键.题型较好,综合性强.

练习册系列答案
相关题目
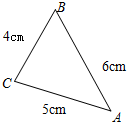 请用两种方法解答下列问题:
请用两种方法解答下列问题: