题目内容
将一个半径为6cm．母线长为15cm的圆锥形纸筒沿一条母线剪开并展平．所得的侧面展开图的圆心角是（ ）度．
分析：根据圆锥的侧面积公式S=πrl得出圆锥侧面积，再结合扇形面积
即可求出圆心角的度数．
| nπR2 |
| 360 |
解答：解：∵将一个半径为6cm，母线长为15cm的圆锥形纸筒沿一条母线剪开并展平，
∴圆锥侧面积公式为：S=πrl=π×6×15=90πcm2，
∴扇形面积为90π=
，
解得：n=144，
∴侧面展开图的圆心角是144度．
故选：D．
∴圆锥侧面积公式为：S=πrl=π×6×15=90πcm2，
∴扇形面积为90π=
| nπ×152 |
| 360 |
解得：n=144，
∴侧面展开图的圆心角是144度．
故选：D．
点评：此题主要考查了圆锥的侧面积公式应用以及与展开图扇形面积关系，求出圆锥侧面积是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
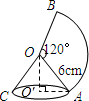如图，将一个半径为6cm，圆心角为120°的扇形薄铁皮AOB卷成圆锥AOC的侧面（接缝无重叠，无缝隙），O′为圆锥的底面圆心，则O′A=