题目内容
以直角坐标系的原点O为圆心，以1为半径作圆．若点P是该圆上第一象限内的一点，且OP与x轴正方向组成的角为α，则点P的坐标为
- A.（cosα，1）
- B.（1，sinα）
- C.（sinα，cosα）
- D.（cosα，sinα）
D
分析：作PA⊥x轴于点A．那么OA是α的邻边，是点P的横坐标，为cosα；PA是α的对边，是点P的纵坐标，为sinα．
解答：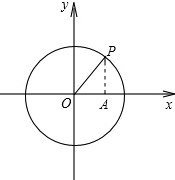
解：作PA⊥x轴于点A，则∠POA=α，
sinα=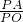
，
∴PA=OP•sinα，
∵cosα=
，
∴OA=OP•cosα．
∵OP=1，
∴PA=sinα，OA=cosα．
∴P点的坐标为（cosα，sinα）
故选D．
点评：解决本题的关键是得到点P的横纵坐标与相应的函数和半径之间的关系．
分析：作PA⊥x轴于点A．那么OA是α的邻边，是点P的横坐标，为cosα；PA是α的对边，是点P的纵坐标，为sinα．
解答：
解：作PA⊥x轴于点A，则∠POA=α，sinα=
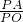，∴PA=OP•sinα，
∵cosα=
，∴OA=OP•cosα．
∵OP=1，
∴PA=sinα，OA=cosα．
∴P点的坐标为（cosα，sinα）
故选D．
点评：解决本题的关键是得到点P的横纵坐标与相应的函数和半径之间的关系．
练习册系列答案
相关题目
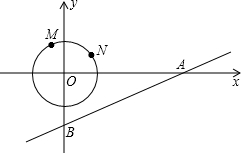如图，以直角坐标系的原点O为圆心作⊙O，点M、N是⊙O上的两点，M（-1，2），N（2，1）
