题目内容
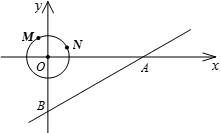
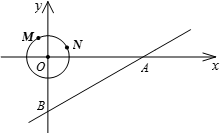
如图，以直角坐标系的原点O作⊙O，点M、N是⊙O上的两点，M（－1，2），N（2，1）
1.试在x轴上找出点P使PM+PN最小，求出P的坐标；
2.若在坐标系中另有一直线AB，A（10，0），点B在y轴上，∠BAO=30°，⊙O以0. 2个单位/秒的速度沿x轴正方向运动，问圆在运动过程中与该直线相交的时间有多长？
【答案】
1.P（1，0）
2.
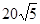秒
【解析】本题考查的是圆的相关特性。
（1）得点M（－1，2）关于X轴的对称点坐标为（－1，－2）。
且在⊙O上，又∵过N（2，1）与（－1，－2）的直线为y=x-1当y=0时，x=1故P（1，0）。
（2）由题意勾股定理得当与直线相切时OA=2半径=2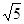
所以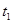
=(10-2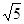)÷0.2，
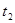=(1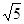0+2)÷0.2
所以t=-=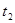
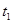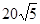
练习册系列答案
相关题目
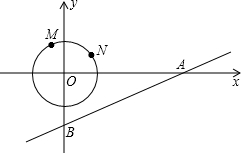如图，以直角坐标系的原点O为圆心作⊙O，点M、N是⊙O上的两点，M（-1，2），N（2，1）
