题目内容
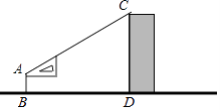
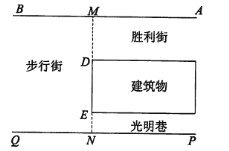
【题目】如图所示,一段街道的两边缘所在直线分别为AB, PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,步行街宽MN为13.4米,建筑物宽DE为6米,光明巷宽EN为2.4米.小亮在胜利街的A处,测得此时AM为12米,求此时小亮距建筑物拐角D处有多远?
【答案】13米.
【解析】
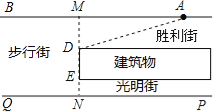
试题连接AD,先根据步行街宽MN为13.4米,建筑物宽DE为6米,光明巷宽EN为2.4米求出MD的长,再根据勾股定理即可得出AD的长.
试题解析:∵AB∥PQ.MN⊥AB,交PQ于点N,MN=13.4米,
DE=6米,EN=2.4米.
∴MD=13.4﹣6﹣2.4=5(米),
∴AD=![]() =
=![]() =13米.
=13米.
答:此时小亮距建筑物拐角D处有13米.

练习册系列答案
相关题目