Question

【题目】某商店经销甲、乙两种商品． 现有如下信息:

请根据以上信息，解答下列问题：

（1）甲、乙两种商品的零售单价分别为 元和 元．（直接写出答案）

（2）该商店平均每天卖出甲商品500件和乙商品1200件．经调查发现，甲种商品零售单价每降0.1元，甲种商品每天可多销售100件．为了使每天获取更大的利润，商店决定把甲种商品的零售单价下降x（x＞0）元．在不考虑其他因素的条件下，当x定为多少时，才能使商店每天销售甲、乙两种商品获取的利润共1700元？

Answer 1

【答案】(1)2，3；（2）0.5元

【解析】

（1）根据图上信息可以得出甲乙商品之间价格之间的等量关系，即可得出方程组求出即可；

（2）根据降价后甲每天卖出：（500+×100）件，每件降价后每件利润为：（1-x）元，即可得出总利润，利用一元二次方程解法求出即可

(1) 解：（1）假设甲、乙两种商品的进货单价各为a，b元，

根据题意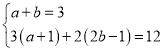得：，解得：，

∴甲零售单价为1+1=2元，乙零售单价为2×2-1=3元，

故答案为：2，3；

（2）(1x)(500+x)+1×1200=1700 即2x2-x=0，

解得x=0.5或x=0(舍去)，

所以当x定为0.5元才能使商店每天销售甲、乙两种商品获取的利润共1700元.