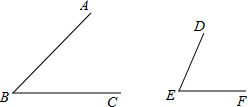题目内容
如图,已知:点O在直线BF上,∠BOD-∠BOC=90°,∠AOC=∠BOD,射线OM平分∠AOF.
(I)∠DOM的度数是多少?为什么?
(II)将图1中的射线OB沿射线OC折叠得到射线OE,如图2,请你在折叠后的图中找出等于2∠DOM的角.
(III)射线ON是将图1中的射线OF绕点O顺时针旋转得到的,如图3,且∠AON=90°,在旋转后的图中互补的角共有多少对?
(I)∠DOM的度数是多少?为什么?
(II)将图1中的射线OB沿射线OC折叠得到射线OE,如图2,请你在折叠后的图中找出等于2∠DOM的角.
(III)射线ON是将图1中的射线OF绕点O顺时针旋转得到的,如图3,且∠AON=90°,在旋转后的图中互补的角共有多少对?

(I)如图1,∠DOM的度数是45°.
理由:∵∠BOD-∠BOC=90°,
∴∠DOC=90°,
∴∠DOF+∠BOC=90°,
∵∠AOC=∠BOD,
∴∠AOD=∠COB,
∵射线OM平分∠AOF,
∴∠AOM=∠MOF,
∴∠AOM+∠AOD=∠DOM=∠MOF+∠BOC=45°;
(II)∵射线OB沿射线OC折叠得到射线OE,
∴∠BOC=∠EOC,
∴∠AOE=∠DOC=90°,
即∠AOE=∠DOC=2∠DOM;
(Ⅲ)∵OM平分∠AOF,
∴∠AOM=∠MOF,
∴∠AOM+∠MOB=180°,
又∵∠AON+∠DOC=90°+90°=180°,
∴∠AON与∠DOC互补,
综上,互补的角有∠AOM与∠MOB,∠AON与∠DOC共2对.
理由:∵∠BOD-∠BOC=90°,
∴∠DOC=90°,
∴∠DOF+∠BOC=90°,
∵∠AOC=∠BOD,
∴∠AOD=∠COB,
∵射线OM平分∠AOF,
∴∠AOM=∠MOF,
∴∠AOM+∠AOD=∠DOM=∠MOF+∠BOC=45°;
(II)∵射线OB沿射线OC折叠得到射线OE,
∴∠BOC=∠EOC,
∴∠AOE=∠DOC=90°,
即∠AOE=∠DOC=2∠DOM;
(Ⅲ)∵OM平分∠AOF,
∴∠AOM=∠MOF,
∴∠AOM+∠MOB=180°,
又∵∠AON+∠DOC=90°+90°=180°,
∴∠AON与∠DOC互补,
综上,互补的角有∠AOM与∠MOB,∠AON与∠DOC共2对.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目