题目内容
等腰三角形的两是方程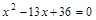
的两根，则这个三角形的周长是：
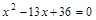的两根，则这个三角形的周长是：| A．17 | B．22 | C．13 | D．17或22 |
B
分析：把方程左边利用十字相乘法分解因式，根据两数积为0，两数至少有一个为0化为两个一元一次方程，分别求出两方程的解得到原方程的解为4或9，然后根据4为腰，4为底边分两种情况考虑，分别根据三角形的边角关系判断满足题意的底边和腰，进而求出三角形的周长．
解答：解：x2-13x+36=0，
因式分解得：（x-4）（x-9）=0，
可得：x-4=0或x-9=0，
解得：x1=4，x2=9，
若4为腰，9为底边，由4+4＜9，得到三边不能构成三角形，故4不能为腰；
若4为底边，9为腰，三角形三边分别为4，9，9，此时三角形周长为4+9+9=22．
故选B
解答：解：x2-13x+36=0，
因式分解得：（x-4）（x-9）=0，
可得：x-4=0或x-9=0，
解得：x1=4，x2=9，
若4为腰，9为底边，由4+4＜9，得到三边不能构成三角形，故4不能为腰；
若4为底边，9为腰，三角形三边分别为4，9，9，此时三角形周长为4+9+9=22．
故选B
练习册系列答案
相关题目
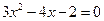
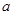是方程
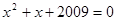的一个根，则代数式
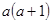的值等于【 】
、
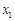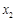是方程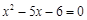
的两个根，则代数式
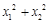的值（ ）
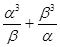的值为 .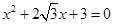
.