��Ŀ����
��2012•�㽭һģ�����о����ɶ���ʱ��ͬѧ�Ƕ�������ͼ1����CBA=90�㣬�ı���ACKH��BCED��ABFG���������Σ�
��1������BK��AE�õ�ͼ2�����CBK�ա�CEA����ʱ����������ȫ�ȵ��ж�������
��2����ͼ1�У��������������Ρ��˻���Ϊ�������Σ��õ�ͼ3��ͬѧ�ǿ���̽����BCD����ABG����ACK�������ϵ��
��3��Ϊ���о��������Ҫ����ͼ1�е�Rt��ABCҲ���С��˻���Ϊ��ǡ�ABC������ȥ������ACKH��ͼ4����AB��BC��������������������BCD������ABG����BCD�����Բ��AD���ڵ�P����ʱC��P��G���ߣ��ӡ�ABC��һ�㵽A��B��C��������ľ���֮����С�ĵ�ǡΪ��P���Ѿ�������֤��������BC=3��CA=4����BCA=60�㣮��PA+PB+PC��ֵ��
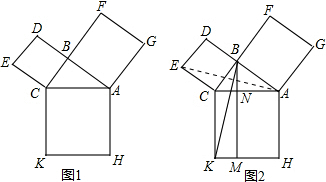

��1������BK��AE�õ�ͼ2�����CBK�ա�CEA����ʱ����������ȫ�ȵ��ж�������
SAS
SAS
����B��BM��KH��M����AC��N����S����KMNC=2S��CKB��ͬ��S������BCED=2S��CEA����S������BCED=S����KMNC��Ȼ���֤�ù��ɶ�������2����ͼ1�У��������������Ρ��˻���Ϊ�������Σ��õ�ͼ3��ͬѧ�ǿ���̽����BCD����ABG����ACK�������ϵ��
S��BCD+S��ABG=S��ACK
S��BCD+S��ABG=S��ACK
����3��Ϊ���о��������Ҫ����ͼ1�е�Rt��ABCҲ���С��˻���Ϊ��ǡ�ABC������ȥ������ACKH��ͼ4����AB��BC��������������������BCD������ABG����BCD�����Բ��AD���ڵ�P����ʱC��P��G���ߣ��ӡ�ABC��һ�㵽A��B��C��������ľ���֮����С�ĵ�ǡΪ��P���Ѿ�������֤��������BC=3��CA=4����BCA=60�㣮��PA+PB+PC��ֵ��


��������1������ȫ�������ε��ж�SAS�ó����ɣ�
��2���ֱ���AB��BC��AC��ʾ�� S��BCD��S��ABG��S��ACK��Ȼ�����AC2=BC2+BA2���ɵó�S��BCD��S��ABG��S��ACK�Ĺ�ϵ��
��3������֤����BPC�ա�BED��AAS���������ó�QC�ij��������ù��ɶ����ó�AD�ij���
��2���ֱ���AB��BC��AC��ʾ�� S��BCD��S��ABG��S��ACK��Ȼ�����AC2=BC2+BA2���ɵó�S��BCD��S��ABG��S��ACK�Ĺ�ϵ��
��3������֤����BPC�ա�BED��AAS���������ó�QC�ij��������ù��ɶ����ó�AD�ij���
����⣺��1������BC=EC����KCB=��ECA��AC=CK���ó���CBK�ա�CEA��SAS����
�ʴ�Ϊ��SAS��
��2����S��ABG=
GE��AB=
��
AB��AB=
AB2��S��BCD=
BC•DM=
��
BC��BC=
BC2��
S��ACK=
AC��NK=
��
AC��AC=
AC2��
��S��BCD+S��ABG=S��ACK��
�ʴ�Ϊ��S��BCD+S��ABG=S��ACK��
��3����PD�Ͻ�ȡPE=PB����BE���ӳ�AC��DQ��AC�ڵ�Q��
�ߡ�BCDΪ�������Σ�BD=BC=CD=3��
���BPD=60�㣬��CPD=60�㣮
���PBE��������
��PB=PC=BE�����BEP=60��
���BED=180��-��BEP=180��-60��=120�㣮
��BPC=��BPD+��DPC=60��+60��=120�㣮
�ڡ�BPC�͡�BED�У�
��
���BPC�ա�BED��AAS����
��PC=DE��
��PA+PB+PC=PA+PE+ED=AD��
�ڡ�CDA�У�CD=3��CA=4���ߡ�DCA=��DCB+��BCA=120�㣮
���DCQ=60�㣬
���QDC=30�㣬
��CQ=
CD=
��3=
��QD=
��
��AQ=4+
=
��
��AD=
=
��
��PA+PB+PC=
��
�ʴ�Ϊ��SAS��
��2����S��ABG=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
S��ACK=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
��S��BCD+S��ABG=S��ACK��
�ʴ�Ϊ��S��BCD+S��ABG=S��ACK��
��3����PD�Ͻ�ȡPE=PB����BE���ӳ�AC��DQ��AC�ڵ�Q��
�ߡ�BCDΪ�������Σ�BD=BC=CD=3��
���BPD=60�㣬��CPD=60�㣮
���PBE��������
��PB=PC=BE�����BEP=60��

���BED=180��-��BEP=180��-60��=120�㣮
��BPC=��BPD+��DPC=60��+60��=120�㣮
�ڡ�BPC�͡�BED�У�
��
|
���BPC�ա�BED��AAS����
��PC=DE��
��PA+PB+PC=PA+PE+ED=AD��
�ڡ�CDA�У�CD=3��CA=4���ߡ�DCA=��DCB+��BCA=120�㣮
���DCQ=60�㣬
���QDC=30�㣬
��CQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
��AQ=4+
| 3 |
| 2 |
| 11 |
| 2 |
��AD=
| DQ2+AQ2 |
| 37 |
��PA+PB+PC=
| 37 |
������������Ҫ������Բ���ۺ�Ӧ���Լ�ȫ�������ε��ж��������Լ����ɶ�����Ӧ�õ�֪ʶ������������Ǻ������QC�ij��������ù��ɶ����ó��ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��2012•�㽭һģ����ͼ��ֱ��a��b����1=50�㣬���2=
��2012•�㽭һģ����ͼ��ֱ��a��b����1=50�㣬���2=