��Ŀ����
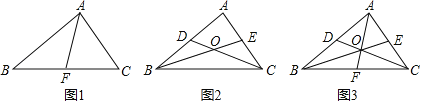
����Ŀ������������ͼ1����ABC�У�AFΪBC���ϵ����ߣ���S��ABF���� ��S��ABC��
����̽����
��1����ͼ2��CD��BE�ֱ��ǡ�ABC�����ߣ�S��BOC��S�ı���ADOE�����
�⣺��ABC�У����������Ľ��ۿɵã�S��BCD��![]() S��ABC��S��ABE��
S��ABC��S��ABE��![]() S��ABC��
S��ABC��
��S��BCD��S��ABE
��S��BCD��S��BOD��S��ABE��S��BOD
��S��BOC��S�ı���ADOE��
��2��ͼ2�У����գ�1���ķ�������˵��S��BOD��S��COE��
��3����ͼ3��CD��BE��AF�ֱ��ǡ�ABC�����ߣ���S��BOC���� ��S��ABC��S��AOE���� ��S��ABC��S��BOD���� ��S��ABF��
������չ��
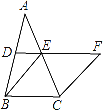
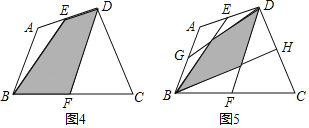
��4������ͼ4��E��F�ֱ�Ϊ�ı���ABCD�ı�AD��BC���е㣬��ֱ��д����Ӱ���ֵ�������ı���ABCD�����֮���������ϵ��S��Ӱ���� ��S�ı���ABCD��
����ͼ5��E��F��G��H�ֱ�Ϊ�ı���ABCD�ı�AD��BC��AB��CD���е㣬��ֱ��д����Ӱ���ֵ�������ı���ABCD�����֮���������ϵ��S��Ӱ���� ��S�ı���ABCD��
���𰸡���������![]() ������̽������2��֤������������3��
������̽������2��֤������������3��![]() ��
��![]() ��
��![]() ��������չ����4����
��������չ����4����![]() ����
����![]() .
.
��������
���������������ߵ����ʼ��ɵó����ۣ�
����̽������2�������������Ľ��ۿɵã�S��BCD��![]() S��ABC��S��BCE��
S��ABC��S��BCE��![]() S��ABC��Ȼ����ݵ�ʽ�Ļ������ʼ��ɵó�S��BOD��S��COE��
S��ABC��Ȼ����ݵ�ʽ�Ļ������ʼ��ɵó�S��BOD��S��COE��
��3���������ߵ����ʺ�̽�����ۣ�1����2�����Ƴ�S��AOE��S��AOD��S��BOF��S��COF��S��BOD��S��COE��![]() S��ABC���Ӷ��ó����ۣ�
S��ABC���Ӷ��ó����ۣ�
������չ����4��������BD���������ߵ����ʿɵ�S��ABE��S��BDE��S��BDF��S��DFC���Ӷ��ó����ۣ�������BD����BE��DG��M��BH��DF��N����������̽������3���Ľ��ۣ��ɵ�S��BDM��![]() S��ABD��S��BDN��
S��ABD��S��BDN��![]() S��BDC�����Ӷ��ó����ۣ�
S��BDC�����Ӷ��ó����ۣ�
�⣺����������AF��BC���ϵ����ߣ�
��S��ABF��S��AFC��
��S��ABF��![]() S��ABC��
S��ABC��
�ʴ�Ϊ![]() ��
��
����̽������2����ABC�У����������Ľ��ۿɵã�S��BCD��![]() S��ABC��S��BCE��
S��ABC��S��BCE��![]() S��ABC��
S��ABC��
��S��BCD��S��BCE
��S��BCD��S��BOC��S��BCE��S��BOC
��S��BOD��S��COE��
��3����CD��BE��AF�ֱ��ǡ�ABC�����ߣ�
��S��BOF��S��COF�� S��BAF��S��CAF��S��BOD��S��AOD��
����̽�����ۣ�1����2����֤��S��BOC��S�ı���ADOE�� S��BOD��S��COE
��S��AOD��S��BAF��S��BOD��S��BOF��S��CAF��S��COE��S��COF��S��AOE
��S��BOC��2S��BOF��S�ı���ADOE��2S��AOD
��S��BOF��S��AOD
��S��AOE��S��AOD��S��BOF��S��COF��S��BOD��S��COE��![]() S��ABC��
S��ABC��
S��BOC��2S��BOF��![]() S��ABC��S��AOE��
S��ABC��S��AOE��![]() S��ABC��S��BOD��
S��ABC��S��BOD��![]() S��ABF��
S��ABF��
�ʴ�Ϊ![]() ��
��![]() ��
��![]() ��
��
������չ����4������ͼ4�У�����BD��

��BE�ǡ�ABD�����ߣ�
��S��ABE��S��BDE��
��DF�ǡ�BCD�����ߣ�
��S��BDF��S��DFC��
��S����![]() S�ı���ABCD��
S�ı���ABCD��
�ʴ�Ϊ![]() ��
��
����ͼ5�У�����BD����BE��DG��M��BH��DF��N��
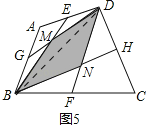
������̽����֪��S��BDM��![]() S��ABD��S��BDN��
S��ABD��S��BDN��![]() S��BDC��
S��BDC��
��S����![]() ��S��ABD+S��BDC����
��S��ABD+S��BDC����![]() S�ı���ABCD��
S�ı���ABCD��
�ʴ�Ϊ![]() ��
��

����Ŀ����20��ײˣ���ÿ��30ǧ��Ϊ������������ķֱ�������������ʾ����¼���£�
��������IJ�(��λ��ǧ��) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
���� | 1 | 4 | 2 | 3 | 2 | 8 |
��1��20��ײ��У����ص�һ��������һ��Ҫ�ض���ǧ��?
��2����������Ƚϣ�20��ײ��ܼƳ����������ǧ��?
��3�����ײ�ÿǧ���ۼ�2Ԫ���������20��ײ˿�������Ԫ?