题目内容
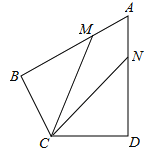
【题目】如图，在四边形ABCD中，AB=CD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上，若AM:MB=AN:ND=1:2，则tan∠MCN=( )
A、
B、
C、
D、
【答案】C．
【解析】
试题解析：∵AB=AD=6，AM：MB=AN：ND=1：2，
∴AM=AN=2，BM=DN=4，
连接MN，连接AC，
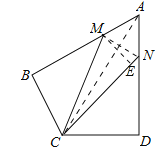
∵AB⊥BC，AD⊥CD，∠BAD=60°
在Rt△ABC与Rt△ADC中，
，
∴Rt△ABC≌Rt△ADC（HL）
∴∠BAC=∠DAC=
∠BAD=30°，MC=NC，
∴BC=AC，
∴AC2=BC2+AB2，即（2BC）2=BC2+AB2，
3BC2=AB2，
∴BC=2
，
在Rt△BMC中，CM=
．
∵AN=AM，∠MAN=60°，
∴△MAN是等边三角形，
∴MN=AM=AN=2，
过M点作ME⊥CN于E，设NE=x，则CE=2
-x，
∴MN2-NE2=MC2-EC2，即4-x2=（2）2-（2-x）2，
解得：x=
，
∴EC=2-=
，
∴ME=
=
，
∴tan∠MCN=
故选C．
练习册系列答案
名校课堂系列答案
相关题目
