题目内容
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
A.x< | B.x<3 | C.x> | D.x>3 |
A.
解析试题分析:先根据函数y=2x和y=ax+4的图象相交于点A(m,3),求出m的值,从而得出点A的坐标,再根据函数的图象即可得出不等式2x<ax+4的解集,∵函数y=2x和y=ax+4的图象相交于点A(m,3),∴3=2m,
m=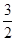 ,∴点A的坐标是(
,∴点A的坐标是(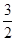 ,3),∴不等式2x<ax+4的解集为x<
,3),∴不等式2x<ax+4的解集为x<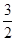 ,故选A.
,故选A.
考点:一次函数与一元一次不等式.

练习册系列答案
相关题目
若点 在函数
在函数 的图象上,则
的图象上,则 ( )
( )
A. &nbs, &nbs, | B. &nbs, &nbs, | C. &nbs, &nbs, | D. &nbs, &nbs, |
某班进行乒乓球比赛,班主任老师为鼓励同学们积极参与,带了50元钱去购买甲、乙两种笔记本作为奖品.已知甲种笔记本每本7元,乙种笔记本每本5元,每种笔记本至少买3本,则该老师购买笔记本的方案共有( )
| A.3种 | B.4种 | C.5种 | D.6种 |
若反比例函数 与一次函数
与一次函数 的图像没有交点,则
的图像没有交点,则 的值可以是( )
的值可以是( )
| A.-2 | B.-1 | C.1 | D.2 |
当 时,正比例函数
时,正比例函数 与反比例函数
与反比例函数 的值相等,则
的值相等,则 与
与 的比是
的比是
| A.4:1 | B.2:1 | C.1:2 | D.1:4 |
关于直线y=-2x,下列结论正确的是( )
| A.图象必过点(1,2) | B.图象经过第一、三象限 |
| C.与y=-2x+1平行 | D.y随x的增大而增大 |
若一次函数 的图象交
的图象交 轴于正半轴,且
轴于正半轴,且 的值随
的值随 值的增大而减小,则( )
值的增大而减小,则( )
A. | B. | C. | D. |
列函数中,y随x的增大而减少的函数是【 】
| A.y=2x+8 | B.y=﹣2+4x | C.y=﹣2x+8 | D.y=4x |
 x+m和y=
x+m和y= x+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是 ( )
x+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是 ( )