Question

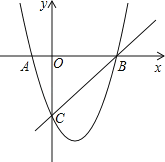
【题目】如图，抛物线y=kx2﹣2kx﹣3k交x轴于A、B两点，交y轴于点C，已知OC=OB．

（1）求抛物线解析式；

（2）在直线BC上求点P，使PA+PO的值最小；

（3）抛物线上是否存在点Q，使△QBC的面积等于6？若存在，请求出Q的坐标；若不存在请说明理由．

Answer 1

【答案】（1）y=x2﹣2x﹣3，（2）（，﹣），（3）存在点Q（﹣1，0）或（4，5），使△QBC面积等于6．

【解析】

试题分析：（1）令y=0可得A，B的坐标，令x=0求出点C的坐标，再根据OC=OB求出k即可得抛物线解析式；

（2）作O的关于BC的对称点O′，连接AO′与BC交于点P，此时PA+PO的值最小，先求出AO′所在的直线与BC所在直线联立可求出交点P的坐标．

（3）在y轴上取一点E（0，1），过点E作ED⊥BC于点D，则△CBE的面积等于6，过点E作EQ平行于BC，交抛物线于点Q，运用直线EQ的解析式与抛物线联立求出点Q的坐标，注意BC下面的另一条与抛物线组成的方程无实根，没有交点．

解：（1）∵抛物线y=kx2﹣2kx﹣3k，

令y=0得0=kx2﹣2kx﹣3k，即0=x2﹣2x﹣3，

解得x1=﹣1，x2=3，

∴A（﹣1，0），B（3，0）

令x=0得y=﹣3k，

∴点C（0，﹣3k），

∵OC=OB，

∴3k=3，解得k=1，

∴抛物线解析式为：y=x2﹣2x﹣3，

（2）如图1，作O的关于BC的对称点O′，连接O′C，O′B，连接AO′与BC交于点P，此时PA+PO的值最小

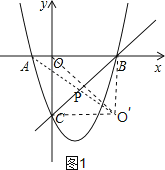
∵OC=OB，OO′⊥BC，

∴BC被OO′平分，

∴四边形OBO′C是正方形，

∴点O′的坐标为（3，﹣3），

∵A（﹣1，0），设AO′所在的直线的解析式为y=kx+b，

∴，解得，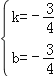

∴AO′所在的直线的解析式为y=﹣x﹣，

由B（3，0），C（0，﹣3）得BC所在直线的解析式为y=x﹣3．

∴联立组成方程组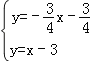，解得，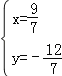

∴直线AO′与直线BC的交点P的坐标为（，﹣），

（3）存在

如图2，

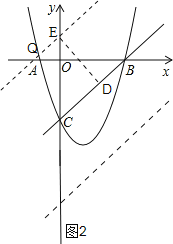
∵△QBC的面积等于6，

∴△QBC的面积=BCh，

∵OC=OB=3

∴BC=3，

∴h=6×2÷3=2．

∵∠OCB=45°，

∴在y轴上取一点E（0，1），过点E作ED⊥BC于点D，则△CBE的面积等于6，过点E作 EQ平行于BC的平行线y=x+1，交抛物线于点Q，

由，解得或，

∴Q（﹣1，0）或（4，5）

同理当E点的坐标为0，﹣7）时直线解析式为：y=x﹣7，

由，得x2﹣3x+4=0，△＜0，方程无实根．

综上存在点Q（﹣1，0）或（4，5），使△QBC面积等于6．