题目内容
(2009•花都区二模)如图,△ABC中,BC=9,∠B=30°,∠C=40°.(1)用尺规作图法作出△ABC的一条高(不写作法,保留作图痕迹);
(2)求出(1)中你所作出的高的长度(精确到0.1);
(3)求△ABC的面积(精确到个位).

【答案】分析:(1)从一个顶点向对边引垂线即可;
(2)利用30度的直角边是斜边的一半计算;
(3)用三角形的面积公式计算.
解答: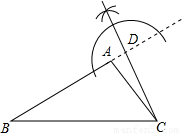 解:
解:
(1)三条高可任作一条,如作AB边上的高CD.
正确画图(3分)
CD为所求作△ABC的一条高.(4分)
(2)解:在Rt△BCD中,BC=9,∠B=30°,
所以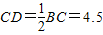 (7分)
(7分)
答:高CD长为4.5.(8分)
(3)解:在Rt△BCD中,BC=9,CD=4.5,
∴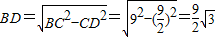 (9分)
(9分)
∵∠CAD=∠B+∠BCA=30°+40°=70°
∴tan∠CAD=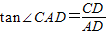
∴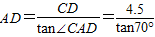 (10分)
(10分)
∴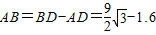 (11分)
(11分)
∴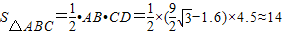
答:△ABC的面积约为14.(12分)
点评:本题综合考查了三角形的高的画法及角直角三角形的能力及三角形的面积公式.
(2)利用30度的直角边是斜边的一半计算;
(3)用三角形的面积公式计算.
解答:
 解:
解:(1)三条高可任作一条,如作AB边上的高CD.
正确画图(3分)
CD为所求作△ABC的一条高.(4分)
(2)解:在Rt△BCD中,BC=9,∠B=30°,
所以
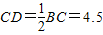 (7分)
(7分)答:高CD长为4.5.(8分)
(3)解:在Rt△BCD中,BC=9,CD=4.5,
∴
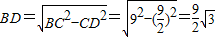 (9分)
(9分)∵∠CAD=∠B+∠BCA=30°+40°=70°
∴tan∠CAD=
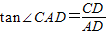
∴
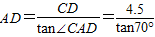 (10分)
(10分)∴
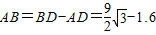 (11分)
(11分)∴
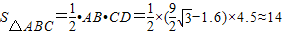
答:△ABC的面积约为14.(12分)
点评:本题综合考查了三角形的高的画法及角直角三角形的能力及三角形的面积公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 .
.