题目内容
(2009•杨浦区二模)如图,在Rt△ABC中,∠C=90°,M为AB边上中点,将Rt△ABC绕点M旋转,使点C与点A重合得到△DEA,设AE交CB于点N.(1)若∠B=25°,求∠BAE的度数;
(2)若AC=2,BC=3,求CN的长.

【答案】分析:(1)根据旋转的性质:旋转前后的图形全等,得到对应角和对应边之间的关系.
(2)根据旋转的性质用同一个未知数表示出有关的边,根据勾股定理列方程计算.
解答:解:(1)∵Rt△ABC绕点M旋转得△DEA,
∴△ABC≌△DEA,且AM=DM,BM=EM,
∴∠DAE=∠C=90°,∠E=∠B=25°,
∵AM=BM,
∴DM=EM,即M为Rt△DEA斜边中点,
∴MA=ME,
∴∠BAE=∠E,
∴∠BAE=25°.
(2)∵∠BAE=∠E,
又∵∠E=∠B,
∴∠BAE=∠B,
∴AN=NB,
设CN=x,则AN=NB=3-x,
在Rt△CAN中,AN2=AC2+CN2,即(3-x)2=4+x2,
解得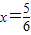 ,即CN=
,即CN= .
.
点评:根据旋转的性质得到对应角和对应边之间的关系是解题的关键.
(2)根据旋转的性质用同一个未知数表示出有关的边,根据勾股定理列方程计算.
解答:解:(1)∵Rt△ABC绕点M旋转得△DEA,
∴△ABC≌△DEA,且AM=DM,BM=EM,
∴∠DAE=∠C=90°,∠E=∠B=25°,
∵AM=BM,
∴DM=EM,即M为Rt△DEA斜边中点,
∴MA=ME,
∴∠BAE=∠E,
∴∠BAE=25°.
(2)∵∠BAE=∠E,
又∵∠E=∠B,
∴∠BAE=∠B,
∴AN=NB,
设CN=x,则AN=NB=3-x,
在Rt△CAN中,AN2=AC2+CN2,即(3-x)2=4+x2,
解得
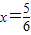 ,即CN=
,即CN= .
.点评:根据旋转的性质得到对应角和对应边之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的斜坡笔直滑下72米,那么他下降的高度为 米.
的斜坡笔直滑下72米,那么他下降的高度为 米.




